7.1 the disjoint set

1. 等价类

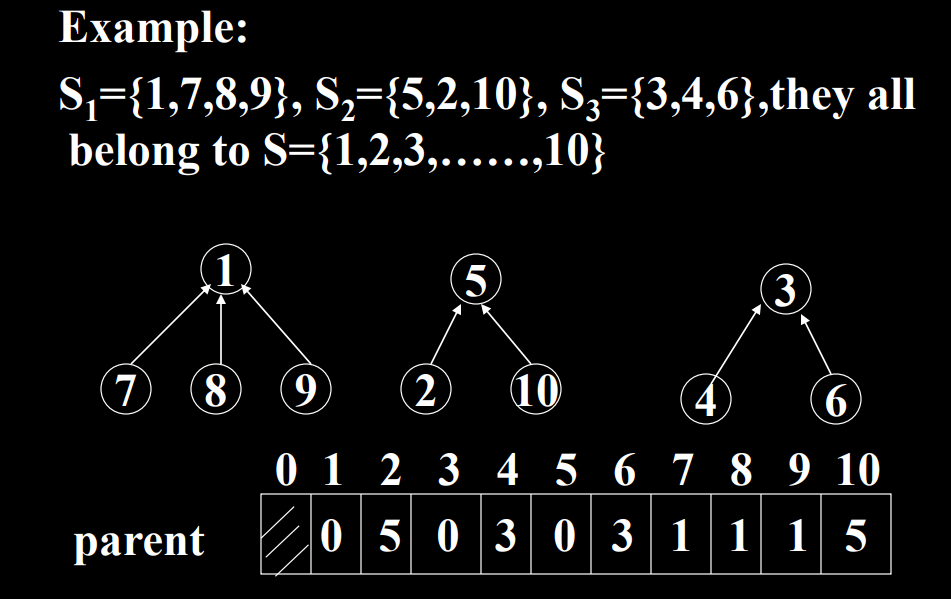
1. 等价类的定义：假设我们有一个n个元素组成的集合U = {1,2,…,n},一个有r个关系的集合R={(i1 ,j1 ), (i2 ,j2 )…… (ir ,jr )}。当且仅当以下条件成立的时候，R才是一个等价类：

   1. Reflexive x ≡ x.(自反性)
   2. Symmetric x ≡ y,y ≡ x(对称性)
   3. Transitive x ≡ y and y ≡ z,then x ≡ z(传递性)

2. EG

   

   

2. 并查集提供的功能

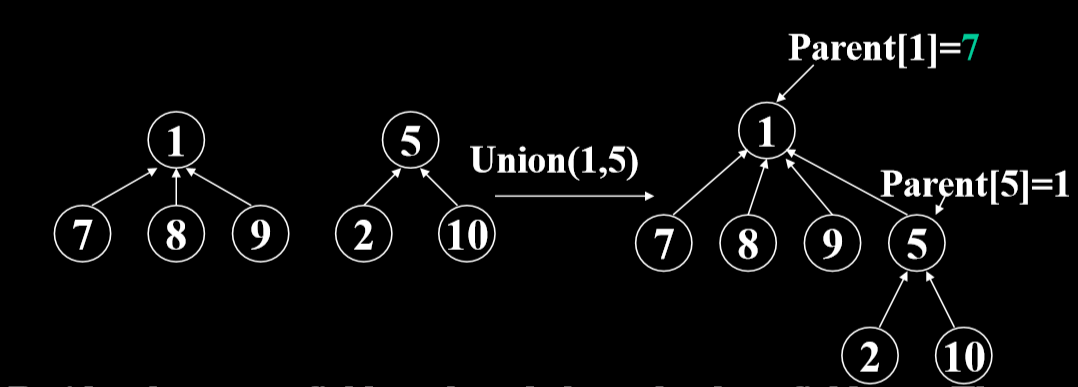
1. Combine(a,b):合并包含元素a和b的两个等价类为一个等价类
2. Find(e):找到包含元素e的等价类

3. 物理实现

1. 并查集的物理实现是通过森林来表示。

   

2. parent数组中存储的值为0的时候，这个结点表示为根结点

3. 所以这个更快速的支持从下向上查询

//simple tree solution to union-find problem 
//使用简单的树结构解决并集的查找问题
void Initialize(int n){
    parent=new int[n+1];
    for(int e=1;e<=n;e++) parent[e]=0;
}
int Find(int e) {
    //向上找到其根结点
    while(parent[e]) e=parent[e];
    return e;
}
void Union(int i, int j) {
    //合并两个结点
    parent[j]=i;
} 

3.1 并集的实现

public class DisjSets {
    public DisjSets( int numElements )
    public void union( int root1, int root2 )
    public int find( int x ) private int [] s;
}
//并查集的构造方法
public DisjSets( int numElements ) {
    s = new int [numElements];
    for( int i = 0; i < s.length; i++ )
        s[i] = -1; //一个根结点
}
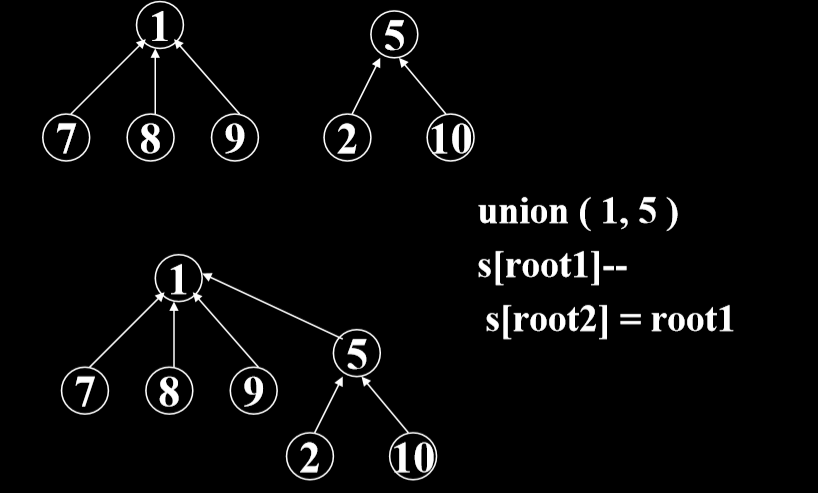
//并查集的合并
public void union( int root1, int root2 ) {
    s[root2] = root1;
}
//并查集的查找，使用递归完成
public int find( int x ) {
    if( s[x] < 0 )
        return x;
    else
        return find( s[x] );
}

3.2 性能估计

1. 算法复杂度

   1. Find– O(h), h 是指树高
   2. Union– θ(1)

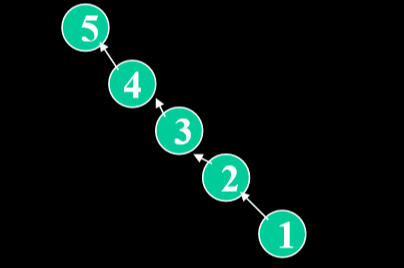
2. 假设我们进行u次组合操作和f次查找操作，f>u，最坏情况下的一颗有m个元素的树可以有高度m

   1. 严重不平衡的树，会影响到查找的时间复杂度

   2. Union(2,1),Union(3,2),Union(4,3),Union(5,4)…

      

3.3 性能提升

1. Weight rule：结点数少的树挂到结点多的树下面
2. Height rule：高度低的树挂到高度高的树的下面

3.3.1 Weight rule

1. 根结点的值代表了weight
2. 为了实现我们新建一个bool类型数组来记录是否是根节点。
3. 除了父字段外，每个节点都有一个布尔字段根。如果当前节点是根节点，则根字段为真。每个根节点的父字段用于统计树中的节点总数。

//Union with the weight rule
void Initialize(int n) {
    root=new bool[n+1];
    parent=new int[n+1];
    for(int e=1;e<=n;e++) {
        parent[e]=1;
        root[e]=true;
    }
}
int Find(int e) {
    while(!root[e])
        e=parent[e];
    return e;
}
void Union(int i, int j) {
    if(parent[i]<parent[j])
    //i becomes subtree of j
    {
        parent[j]=parent[j]+parent[i];
        root[i]=false;
        parent[i]=j;
    } else {
        parent[i]=parent[i]+parent[j];
        root[j]=false;
        parent[j]=i;
    }
}

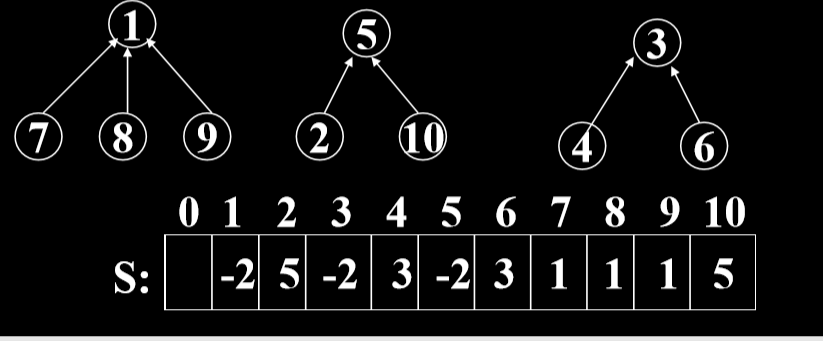
其实也可以省去标记根的数组，用负数来表示weight即可。

3.3.2 Height rule

使用负数来记录树高

//java
public void union( int root1, int root2 ) { 
    if(s[root2] < s[root1])
        s[root1] = root2;
    else {
        if(s[root1] == s[root2] )
            s[root1]--;
        s[root2] = root1;
    }
}//注意到负数会都反过来

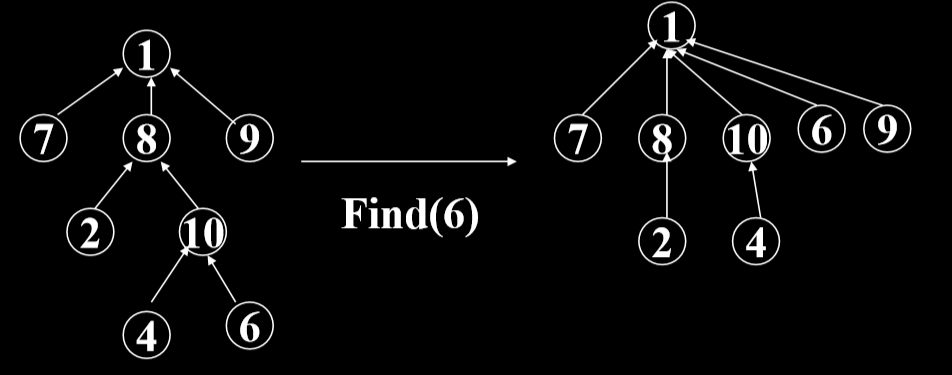
3.3.3 find

改进并查集以减少每次查找所需的时间，从而使树的高度不会线性增加

//java是用来记录树高
public int find(int x) {
    if( s[x] < 0 )
        return x;
    else
        return s[x] = find(s[x]);
}