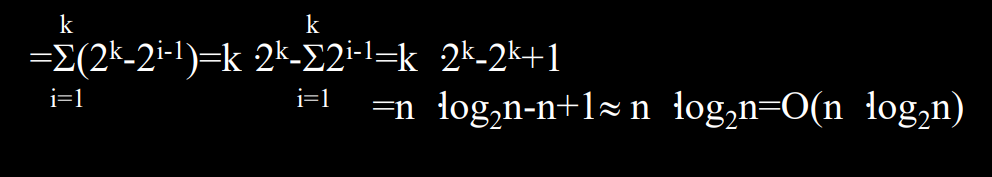7.0 sorting

发表于 2023/12/23

作者 Sa1i3ri 28 分钟阅读

1. 概述

排序：n个对象的序列R[0],R[1],R[2],…R[n-1] 按其关键码的大小，进行由小到大(非递减)或由大到小(非递增)的次序重新排序的。
关键码(key)：进行排序的根据
两大类：
1. 内排序：对内存中的n个对象进行排序。
2. 外排序：内存放不下，还要使用外存的排序。(在本节中暂不考虑)
排序算法的稳定性：如果待排序的对象序列中，含有多个关键码值相等的对象，用某种方法排序后，这些对象的相对次序不变的，则是稳定的，否则为不稳定的。
例： 35 8~1~ 20 15 8~2~ 28
8~1~ 8~2~ 15 20 28 35 稳定的
排序种类
1. 内排序
  - 插入排序，交换排序，选择排序，归并排序，基数排序
2. 外排序:本章暂不讨论外排序
排序的算法分析
1. 时间开销 — 比较次数，移动次数
2. 所需的附加空间 - 空间开销
下面是静态排序过程中所用到的数据表类定义：

1.2 类定义

  
const int DefaultSize=100;
template<class Type>class datalist;
template<class Type>class Element{ 
    private:
        Type key;
        field otherdata;
    public:
        Type getkey( ){return key;}
        void setKey(const Type x){key=x;} 
        Element<Type>&operator=(Element<Type> &x ){ this = x; } 
        int operator ==(Type & x){return !(this < x||x < this);}
        int operator !=(Type & x){return this < x||x < this;}
        int operator <= (Type & x){return !(this > x);}
        int operator >=(Type & x){return!(this < x);}
        int operator < (Type & x){return  this > x;}
};
template<class Type> class datalist {
    public:
        datalist(int MaxSz=DefaultSize):MaxSize(MaxSz),CurrentSize(0){
            vector=new Element<Type>[MaxSz];
        } 
        void swap (Element <Type> & x, Element<Type> & y){Element <Type> temp=x; x=y; y=temp;}
    private:
        Element <Type> * vector;
        int MaxSize, CurrentSize;
};

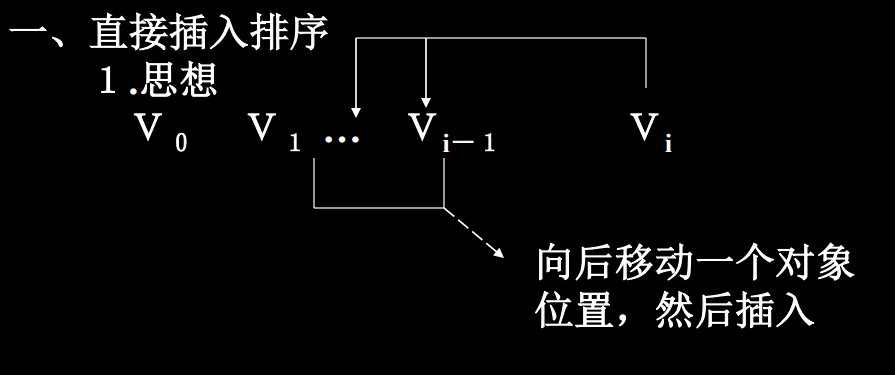
2. 插入排序

排好前面两个，然后在后面的部分进行插入排序。
思想:思想：Ｖ₀，Ｖ₁，…，V_i-1个对象已排好序，现要插入Ｖ~i~到适当位置
- 例子：体育课迟到的人
方法：直接插入排序，链表插入排序，折半插入排序，希尔排序

2.1 直接插入排序

2.1.1 思想

2.1.2 代码实现

  
//java
public static void Insert( int [] a , int n, int x) {
    //Insert x into the sorted array a[0:n-1] 
    int i;
    //把比x大的数集体向后移，从后向前比较
    for(i=n-1; i>=0 && x<a[i]; i--){
        a[i+1]=a[i]; 
    }
    //现在a[i]<=x
    a[i+1]=x;//注意这句话不在for循环中
}
public static void InsertionSort( int [] a,  int n) {
    for(int i=0; i<n; i++) {
        int t = a[i];
        //a[i]是第i+1个值
        Insert(a,i,t);
    }
}

  
//Another version of insertion sort
public static void InsertionSort(int []a, int n) {
    for(int i=0;i<n;i++){
        //insert a[i] into a[0:n-1]
        int t=a[i];
        int j;
        for(j=i-1; j>=0&&t<a[j]; j--)
            a[j+1]=a[j];
        a[j+1]=t;
        //比前面大后推一格
    }
}

  
template<class Type> void InsertionSort(datalist<Type> & list) {
    for (int i=1; i<list.CurrentSize; i++)
        Insert(list, i);
}
template<class Type> void Insert(datalist<Type> & list, int i) {
    Element<Type> temp=list.vector[i];
    int  j=i ;
    while(j>0&&temp.getkey()<list.vector[j-1].getkey()){
        list.Vector[j]=list.Vector[j-1];
        j--;
    }
    list.Vector[j]=temp;
}

2.1.3 复杂度

O(n^2^)

2.1.4 稳定性

稳定的

2.2 折半插入排序(Binary Insert Sort)

也称二分法插入排序

2.2.1 思想

不需要逐一去比较大小，而是去比较已排序序列的中位数，这个中间的位置将一排序列分为左右两部分，通过一次比较后，就缩小了比较的范围，重复这样的操作，需要插入的元素就找到了合适的位置了。

#### 2.2.2 代码实现

  
//C++
//可以使用递归，也可以不使用递归
template <class Type> void BinaryInsertSort( datalist<Type> &list) {
    for (int i=1;i<list.currentSize;i++) 
        BinaryInsert(list, i);
}                                         
template <class Type> void BinaryInsert( datalist<Type> &list, int i) {
    int left=0, Right=i-1; 
    Element<Type>temp = list.Vector[i]; 
    while (left<=Right) {
        //调整区间
        int middle=(left+Right)/2;
        if (temp.getkey()<list.Vector[middle].getkey())
            Right=middle-1;
        else
            left=middle+1;
    }
    //不论何种情况，现在left所在下标永远是应该要插入的下标（why？思考上图的28变成16会怎么操作）
    
    for(int k=i-1;k>=left;k--)
        list.Vector[k+1]=list.Vector[k];
    
    list.Vector[left]=temp;
}

2.2.3 复杂度

O(n logn)

2.2.4 稳定性

稳定的

2.3 希尔排序(Shell Sort)

又称缩小增量排序(diminishing - increament sort)

2.3.1 思想

取一增量(间隔gap < n)，按增量分组，对每组使用直接插入排序或其他方法进行排序。
减少增量(分的组减少，但每组记录增多)。直至增量为1，即为一个组时。

每次完成排序后，gap每次都取一半。

2.3.2 代码实现

  
//c++
void ShellInsert(vector<int> &list, const int gap) {
    for (int i = gap; i < list.size(); i++) {
        auto temp = list[i];
        int j = i;
        //对gap中的数进行排序
        while (j >= gap && temp<list[j-gap]) {
            list[j] = list[j - gap];
            j -= gap;
        }
        list[j] = temp;
    }
}


void Shellsort(vector<int>&list) {
    int gap=list.size()/2;
    while (gap) {
        ShellInsert(list, gap);
        gap= gap==2? 1 : (int)(gap/2);
    }
}

  
//java
public static void shellsort( Comparable [ ] a ) {
    for (int gap = a.length/2 ; gap>0 ; gap/=2 )
        for (int i = gap; i < a.length; i++) {
            //遍历一遍
            Comparable tmp = a[i];
            int j = i;
            for (;j >= gap && tmp.compareTo( a[j-gap] )< 0;j -= gap )
                //完成一遍下滤
                a[j] = a[j – gap];
            a[j] = tmp;
    }
}

2.3.3 复杂度

与选择的缩小增量有关，但到目前还不知如何选择最好结果的缩小增量序列。
平均比较次数与移动次数大约n^1.3左右

2.3.4 稳定性

不稳定的

3. 交换排序

方法的本质：不断的交换反序的对偶，直到不再有反序的对偶为止。
两种方法：
1. 冒泡排序(Bubble sort)
2. 快速排序(Quick sort)

3.1 冒泡排序

3.1.1 思想

每次遍历一次数组，然后仅仅比较相邻的两个数字，把最大的或最小的冒上去
然后遍历n次

3.1.2 代码实现

  
//java
public static void Bubble( int [ ] a , int n) {
    //Bubble largest element in a[0:n-1] to right 
    for(int i=0; i<n-1; i++) 
        if(a[i] > a[i+1])
            swap(a[i],a[i+1]);
    }
public static void BubbleSort( int [ ] a, int n) {  
    //Sort a[0:n-1] using a bubble sort 
    for(int i=n ;i>1; i--) 
        Bubble(a,i); 
}

  
//C++
template<class Type> void  BubbleSort( datalist<Type> & list) {
    int pass=1;
    int exchange=1;
    while (pass<list.CurrentSize &&exchange) {
        BubbleExchange(list, pass, exchange);
        pass++;
    }
}
template<class Type>  void  BubbleExchange(datalist<Type> &list, const int i, int & exchange) {
    exchange=0;
    for (int j=list.CurrentSize-1; j>=i; j--)
        if (list.Vector[j-1].getkey()>list.Vector[j].getkey()) {
            swap(list.Vector[j-1],  list.Vector[j]);
            exchange=1;
        }
}

3.1.3 复杂度

O(n^2^)

3.1.4 稳定性

稳定的

3.2 快速排序

3.2.1 思想

在n个对象中，取一个对象(如第一个对象——基准pivot)，按该对象的关键码
1. 把所有小于等于该关键码的对象分划在它的左边。
2. 大于该关键码的对象分划在它的右边。
对左边和右边(子序列)分别再用快速排序。

3.2.2 代码实现

  
/*
    left:数组左边界
    right：数组右边界
    */
    public void quickSort(int[] arr, int left, int right){
        if(left < right){
            int pos = partition(arr, left, right);
            quickSort(arr, left, pos - 1);
            quickSort(arr, pos + 1, right);
        }
    }
    public int partition(int[] arr, int left, int right){
        int base = arr[left];
        while(left < right){
            while(left < right && arr[right] >= base){
                right--;
            }
            arr[left] = arr[right];
            while(left < right && arr[left] <= base){
                left++;
            }
            arr[right] = arr[left];       
        }
        arr[left] = base;
        return left;
    }
}

  
//c++
template <class Type> void QuickSort( datalist <Type>& list, const int left,  const int right ) {
    if (left<right) {
        int pivotpos = partition(list, left, right);
        QuickSort(list, left, pivotpos-1);
        QuickSort(list, pivotpos+1, right);
    }
}
//partition
template <class Type> int partition(datalist<Type> &list, const int low, const int high) {
    int i=low,j=high;  
    //privot就是base
    Element<Type>pivot=list.Vector[low];
    while (i != j ) {
        while(list.Vector[j].getkey()>pivot.getkey( ) && i<j)
            j--;
        if (i<j) {
            list.Vector[i]=list.Vector[j];
            i++;
        }
        while(list.Vector[i].getkey()<pivot.getkey( ) && i<j)
            i++;
        if (i<j) {
            list.Vector[j]=list.Vector[i];
            j--;
        }
    }
    list.Vector[i]=pivot;
    return i;
}

  
public static void quicksort( Comparable [ ] a){
    quicksort(a, 0, a.length – 1);
}
private static Comparable median3(Comparable [ ] a, int left, int right ) {
    int center = ( left + right ) / 2;
    if ( a[center].compareTo( a[left ] < 0 )
        swapReferences( a, left, center );
    if ( a[ right ] . compareTo( a[left ]) < 0 )
        swapReferences( a, left, right );
    if( a[right ].compareTo( a[ center ] ) < 0 ) swapReferences( a, center, right );
    //调整了到最后一个位置上
    swapReferences( a, center, right – 1 );
    return a[ right – 1 ];
}
private static void quicksort( Comparable [ ] a, int left, int right ) {
    if( left + CUTOFF <= right ) {   
        Comparable pivot = median3( a, left, right );
        int i = left, j = right – 1;
        for(;;) {
            while(a[ ++i ].comparaTo( pivot  ) < 0 ){}
            while(a[--j].compareTo( pivot ) > 0 ) { }
            if(i < j)
                swapReferences( a, i, j ); 
            else
                break;
        }
        swapReferences(a,i,right – 1);
        quicksort( a, left, i – 1 );
        quicksort( a, i + 1, right );
    } else
        insertionSort( a, left, right );
}

3.2.3 复杂度

O(n logn)

3.2.4 稳定性

不稳定的

3.2.5 避免有序情况

如果数组是非常无序，杂乱无章的，那么快速排序的效率是非常高的

可是如果数列有序，往往快速排序的时间复杂度便由O(nlogn)退化到O(n^2^)

方法1：随机选取pivot, 但随机数的生成一般是昂贵的。
方法2：三数中值分割法(Median-of-Three partitioning) N个数，最好选第(N/2)(向上取整)个最大数，这是最好的中值，但这是很困难的。一般选左端、右端和中心位置上的三个元素的中值作为枢纽元。
- 8, 1, 4, 9, 6, 3, 5, 2, 7, 0 (取8, 6, 0)
- 具体实现时：将 8，6，0 先排序，即 0, 1, 4, 9, 6, 3, 5, 2 , 7, 8, 得到中值pivot为 6
分割策略:
1. 将pivot与最后倒数第二个元素交换，使得pivot离开要被分割的数据段。然后，i 指向第一个元素，j 指向倒数第二个元素。
  - 0, 1, 4, 9, 7, 3, 5, 2, 6, 8
2. 然后进行分划
图解排序算法(五)之快速排序——三数取中法 - dreamcatcher-cx - 博客园 (cnblogs.com)

  
public static void quicksort( Comparable [ ] a) 
{ 
    quicksort( a, 0, a.length – 1 );
}
private static Comparable median3( Comparable [ ] a, int left, int right )
{ 
    int center = ( left + right ) / 2;
    if ( a[center].compareTo( a[left ]） < 0 )
        swapReferences( a, left, center );
    if ( a[ right ] . compareTo( a[left ]) < 0 )
        swapReferences( a, left, right );
    if( a[right ] . compareTo( a[ center ] ) < 0 )
		swapReferences( a, center, right );
		swapReferences( a, center, right – 1 );
	return a[ right – 1 ];
} 
//8, 1, 4, 9, 6, 3, 5, 2, 7, 0 ——> 0, 1, 4, 9, 7, 3, 5, 2, 6, 8
private static void quicksort( Comparable [ ] a, int left, int right )
{ 
    if( left + CUTOFF <= right ){ 
        Comparable pivot = median3( a, left, right );
		int i = left, j = right – 1;
		for( ; ; ){ 
        while( a[ ++i ] . comparaTo( pivot ) < 0 ) { }
		while( a[ --j ] . compareTo( pivot ) > 0 ) { }
		if( i < j ){
           swapReferences( a, i, j ); 
        }else{
           break;
        }
	}
	swapReferences( a, i, right – 1 );
	quicksort( a, left, i – 1 );
	quicksort( a, i + 1, right );
	}else{
        insertionSort( a, left, right );
    }

}

4. 选择排序

每次找到数组中的最小值找到然后放到前面，进行重复递归。
也可以将最大的数字找出来然后当放到后面。

4.1 直接选择排序

4.1.1 思想

首先在n个记录中选出关键码最小(最大)的记录，然后与第一个记录(最后第n个记录)交换位置，再在其余的n-1个记录中选关键码最小(最大)的记录，然后与第二个记录(第n-1个记录)交换位置，直至选择了n－1个记录。

4.1.2 代码实现

  
//java
public static void SelectionSort(int [] a, int n) {
    //sort the n number in a[0:n-1].
    //找到大数字放置到后面
    for(int size = n; size>1; size--){
        //n-1
        int j = Max(a,size);
        //n-1+n-2+...+1
        swap(a[j],a[size-1]);
    }
} 

  
//c++
template <class Type> void SelectSort(datalist<Type> &list) {
    for ( int i=0; i<list.CurrentSize-1; i++)
        SelectExchange(list, i);
}
template <class Type> void SelectExchange( datalist<Type> & list, const int i) {
    int k=i;
    for ( int j=i+1; j<list.CurrentSize; j++)
        if (list.Vector[j].getkey( )<list.Vector[k].getkey( ))
            k=j;
    if ( k!=i)
        Swap(list.Vactor[i], list.Vector[k]);
}

4.1.3 复杂度

O(n^2^)

4.1.4 稳定性

不稳定的

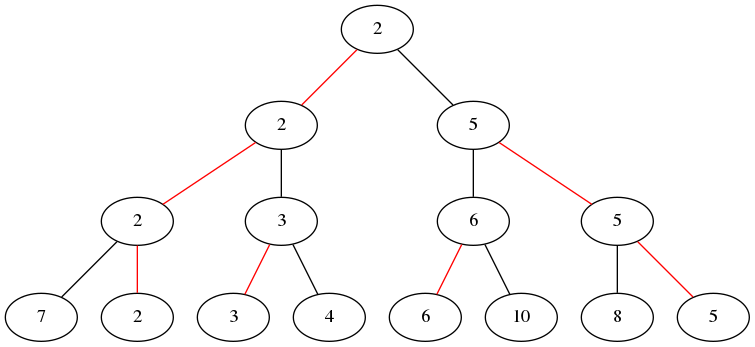
4.2 锦标赛排序（树形选择排序）

直接选择排序存在重复做比较的情况，锦标赛排序克服了这一缺点。

4.2.1 思想

具体方法:

n个对象的关键码两两比较得到(n/2)(向上取整)个比较的优胜者(关键码小者)保留下来, 再对这(n/2)(向上取整)个对象再进行关键码的两两比较, ……直至选出一个最小的关键码为止。如果n不是2的K次幂，则让叶结点数补足到满足 2^k < n <= 2^k个。
输出最小关键码。再进行调整：即把叶子结点上，该最小关键码改为最大值后，再进行由底向上的比较，直至找到一个最小的关键码(即次小关键码)为止。重复2，直至把关键码排好序。

4.2.2 代码实现

  
int n, a[maxn], tmp[maxn << 1];

int winner(int pos1, int pos2) {
  int u = pos1 >= n ? pos1 : tmp[pos1];
  int v = pos2 >= n ? pos2 : tmp[pos2];
  if (tmp[u] <= tmp[v]) return u;
  return v;
}

void creat_tree(int &value) {
  for (int i = 0; i < n; i++) tmp[n + i] = a[i];
  for (int i = 2 * n - 1; i > 1; i -= 2) {
    int k = i / 2;
    int j = i - 1;
    tmp[k] = winner(i, j);
  }
  value = tmp[tmp[1]];
  tmp[tmp[1]] = INF;
}

void recreat(int &value) {
  int i = tmp[1];
  while (i > 1) {
    int j, k = i / 2;
    if (i % 2 == 0 && i < 2 * n - 1)
      j = i + 1;
    else
      j = i - 1;
    tmp[k] = winner(i, j);
    i = k;
  }
  value = tmp[tmp[1]];
  tmp[tmp[1]] = INF;
}

void tournament_sort() {
  int value;
  creat_tree(value);
  for (int i = 0; i < n; i++) {
    a[i] = value;
    recreat(value);
  }
}

4.2.3 复杂度

O(n logn)

4.2.4 稳定性

稳定的

4.3 堆排序

参考Heap部分

4.3.1 思想

第一步，建堆，根据初始输入数据，利用堆的调整算法FilterDown()，形成初始堆。(形成最大堆)
第二步，一系列的对象交换和重新调整堆

4.3.2 代码实现

  
//c++
Template<class  Type>void HeapSort(datalist<Type>&list) {
    for(int i=(list.currentsize-1)/2;i>=0;i--)
        FilterDown(i,list.currentsize-1);
    for(i=list.currentsize-1;i>=1;i--){
        Swap(list.Vector[0],list.vector[i]);
        FilterDown(0,i-1);
    }
}

  
//java program
public static void heapsort( Comparable []a) {
    for( int i = a.length / 2; i >= 0; i-- )
        percDown( a, i, a.length );
    for( int i = a.length – 1; i > 0; i-- ) {
        swapReferences( a, 0, i );
        percDown( a, 0, i);
    }
}
private static int leftChild( int i ) {   
    return 2 * i + 1;
}
private static void percDown( Comparable [ ] a, int  i,  int n ) {
    int child;
    Comparable tmp;
    for( tmp = a[i];leftChild(i) < n ; i = child ) {
        child = leftchild( i );
        if( child!=n – 1&& a[child].compareTo( a[ child + 1 ] ) < 0 )
            child ++;
        if( tmp . compareTo( a[ child ] < 0 )
            a[ i ] = a[ child ];
        else
            break;
    }
    a[i] = tmp;
}

4.3.3 复杂度

O(n logn)

4.3.4 稳定性

不稳定的

5. 秩排序(Rank sort)

重新启用一个数组，用来记录相应的排名

5.1 代码实现

  
public static void Rank( int [] a, int n, int [] r) {
    //Rank the n elements a[0:n-1]
    for(int i=0;i<n;i++){
        r[i]=0;
    }
    //首先将全部的数字重置为0
    for(int i=1;i<n;i++)
        for(int j=0;j<i;j++)
            if(a[j]<=a[i])
                r[i]++;
            else
                r[j]++;
            //胜者排名不需要向后增加，而败者需要增加次序。
}
public static void Rearrange( int [ ]a, int n, int[ ] r) {
    //In-place rearrangement into sorted order
    for(int i=0;i<n;i++)
        while(r[i]!=i) {
            //在数组[n]上的应该是第n+1大的数字
            int t=r[i];
            swap(a[i],a[t]);
            swap(r[i],r[t]);
        }
}

6. 基数排序(Radix Sort)

先取个位数，按照个位数来放到十个桶里面。
- 根据先后次序进图桶
按照十位数，继续放入桶中，根据个位排序结果
重复上述操作，直到最高位。
原理:每次让这一位的从前往后排序。

7. 归并排序

7.1 思想

归并：两个(多个)有序的文件组合成一个有序文件
方法：每次取出两个序列中的小的元素输出之；当一序列完，则输出另一序列的剩余部分

7.2 代码实现

  
//c++
template<class Type> void merge(datalist<Type> & initList, datalist<Type>& mergedList, const int l, const int m, const int n) {
    int i=l, j=m+1, k= l;
    while ( i<=m && j<=n ) if (initList.Vector[i].getkey( )<initList.Vector[j].getkey( )) {
        mergedList.Vector[k]=initList.Vector[i];
        i++;
        k++;
    }
    else{
        mergedList.Vector[k]=initList.Vector[j];
        j++;
        k++;
    }
    if (i<=m)
        for (int n1=k, n2=i; n1<=n && n2<=m;  n1++, n2++)
            mergedList.Vector[n1]=initList.Vector[n2];
    else
        for(int n1=k, n2=j; n1<=n && n2<=n; n1++, n2++)
            mergedList.Vector[n1]=initList.Vector[n2];
}

7.3 迭代的归并排序算法

n个长为1的对象两两合并，得n/2个长为2的文件
n/2个长为 2………………….得n/4个长为4的文件…
2个长为n/2的对象两两合并,得1个长为n的文件

7.3.1 代码实现

  
//c++
template <class Type> void MergeSort(datalist <Type> & list) {
    datalist <Type> tempList(list.MaxSize); 
    int len=1;
    while (len<list.CurrentSize) {
        MergePass(list, tempList, len); len *=2 ;
        if (len >= list.CurrentSize) {
            for (int i=0;i< list.CurrentSize; i++)
                list.Vector[i]=tempList.Vector[i];
        }else{
            MergePass(tempList, list, len); len*=2;
        }
    }
    delete[]tempList;
}

当两段均满len长时调用merge
当一长一短时也调用merge(但第二段的参数不同)
当只有一段时，则复抄
块合并算法实现

  
//c++
template <class Type> void MergePass( datalist<Type> & initList, datalist <Type> & mergedList, const int len) {
    int i=0;
    while (i+2*len<=initList.CurrentSize-1) {
        merge( initList, mergedList, i, i+len-1, i+2*len-1);
        i+=2*len;
    }
    if(i+len <= initList.CurrentSize-1)
        merge(initList, mergedList, i, i+len-1,initList.CurrentSize-1);//因为有可能有块长度为余数，并不满足结果的，所以要额外处理
    else
        for( int j=i ; j<= initList.CurrentSize; j++)
            mergedList.Vector[j]=initList.Vector[j];
}

  
//java
public static void mergeSort( Comparable [ ] a ) {
    Comparable [ ] tmpArray = new Comparable[a.length];
    mergeSort( a, tmpArray, 0, a.length – 1 );
}                            
private static void mergeSort( Comparable [ ] a, Comparable [] tmpArray, int left, int right ) {
    if( left < right ) {
        int center = ( left + right ) / 2;
        mergeSort(a, tmparray, left, center );
        mergeSort(a, tmpArray, center + 1, right );
        merge( a, tmpArray, left, center + 1, right );
    }
}
private static void merge( Comparable [ ] a, Comparable [] tmpArray, int leftPos, int rightPos, int rightEnd ) {
    int leftEnd = rightPos – 1;
    int tmpPos = leftPos;
    int numElements = rightEnd – leftPos + 1;
    while( leftPos <= leftEnd && rightPos <= rightEnd )
        if( a[ leftPos ].compareTo( a[ rightPos ] ) <= 0 )
            tmpArray[ tmpPos++ ] = a[ leftPos++ ];
        else
            tmpArray[ tmpPos++ ] = a[ rightPos++ ];
    while( leftPos <= leftEnd )
        tmpArray[ tmpPos++ ] = a[ leftPos++ ];
    while( rightpos <= rightEnd)
        tmpArray[ tmpPos++] = a[ rightpos++ ];
    for( int i = 0; i < numElements; i++, rightEnd-- )
        a[ rightEnd ] = tmpArray[ rightEnd ];
}     

7.3.2 复杂度

O(n logn)

7.3.3 稳定性

稳定的

7.4 递归的归并排序算法

使用静态链表的方法来实现

7.3.1. 算法实现

主程序 mergesort(L)
子程序 divide(L,L1)，将L划分成两个子表 3.合并两有序序列 merge(L,L1)

  
void MergeSort (List <Type> &L) {
    List <Type> L1;
    if (L.first!=NULL)
        if (L.first->link != NULL)//至少有两个结点
        {
            divide (L, L1);
            MergeSort(L);
            MergeSort(L1);
            L=merge( L, L1);
        }
}

7.3.2. 有序链表的merge算法

  
//c++
List<Type> & merge (List<Type> &L1, List<Type> & L2) {
    ListNode<Type>*p=L1.first,*q=L2.first,  *r ;
    List<Type> temp;
    if ((p= =NULL) or (q= =NULL)) {
        if (p!=NULL){
            temp.first=p;
            temp.last=L1.last;
        }else{
            temp.first=q;
            temp.last=L2.last;
        }
    }else{
        if (p->data<=q->data) {
            r = p;
            p = p->link;
        }else{
            r = q;
            q = q->link;
        }
        temp.first = r ;
        while((p!=NULL) && (q!=NULL)) {
            if (p->data<=q->data) {
                r->link=p;
                r=p;
                p=p->link;
            }else{
                r->link=q;
                r=q;
                q=q->link;
            }
        }
        if (p= =NULL){
            r->link=q;
            temp.last=L2.last;
        }else {
            r->link=p;
            temp.last=L1.last;
        }
    }
    return temp;
}

7.3.3. 下面讨论divide(List&L1,ListL2)

将L1表分为两个长度几乎相等的表，L1.first指向前半部分，L2.first指向后半部分，要求被划分的表至少含有两个结点。

方法：设两个流动指针p,q指向表的结点一般来讲让p前进一步，q前进二步，最后当q= NULL时，这时p 恰好指向前半张表的最后一个结点。
Eg.如果有10个结点，p走5次，q走10次正好走到表末尾

  
void divide(List<Type> & L1, List <Type> & L2) {
    ListNode <Type> *p, *q;
    L2.last=L1.last;
    p=L1.first;
    q=p->link;
    q=q->link;
    while (q!=NULL) {
        p=p->link;
        q=q->link;
        if (q!=NULL)
            q=q->link;
    }
    q=p->link;
    p->link=NULL;
    L1.last=p;
    L2.first=q;
}

8. 总结

大二上, 数据结构与算法

课内笔记大二上数据结构与算法

本文由作者按照 CC BY 4.0 进行授权

1. 概述

1.2 类定义

2. 插入排序

2.1 直接插入排序

2.1.1 思想

2.1.2 代码实现

2.1.3 复杂度

2.1.4 稳定性

2.2 折半插入排序(Binary Insert Sort)

2.2.1 思想

2.2.3 复杂度

2.2.4 稳定性

2.3 希尔排序(Shell Sort)

2.3.1 思想

2.3.2 代码实现

2.3.3 复杂度

2.3.4 稳定性

3. 交换排序

3.1 冒泡排序

3.1.1 思想

3.1.2 代码实现

3.1.3 复杂度

3.1.4 稳定性

3.2 快速排序

3.2.1 思想

3.2.2 代码实现

3.2.3 复杂度

3.2.4 稳定性

3.2.5 避免有序情况

4. 选择排序

4.1 直接选择排序

4.1.1 思想

4.1.2 代码实现

4.1.3 复杂度

4.1.4 稳定性

4.2 锦标赛排序（树形选择排序）

4.2.1 思想

4.2.2 代码实现

4.2.3 复杂度

4.2.4 稳定性

4.3 堆排序

4.3.1 思想

4.3.2 代码实现

4.3.3 复杂度

4.3.4 稳定性

5. 秩排序(Rank sort)

5.1 代码实现

6. 基数排序(Radix Sort)

7. 归并排序

7.1 思想

7.2 代码实现

7.3 迭代的归并排序算法

7.3.1 代码实现

7.3.2 复杂度

7.3.3 稳定性

7.4 递归的归并排序算法

7.3.1. 算法实现

7.3.2. 有序链表的merge算法

7.3.3. 下面讨论divide(List&L1,ListL2)

8. 总结

热门标签