6.0 Priority Queues

1. 优先级队列

1. 一个优先级队列是0个或者更多元素的集合。每一个元素都有一个优先级或者值

2. 进入队列的时候有优先级，出队列优先出高优先级的.

   以下我们确定元素的优先级是通过数字的大小来确定。

1.1 优先级队列分类(根据大小)

1. 在最小优先级队列（min priority queue）中，当需要删除一个元素的时候，我们找到优先级最小的元素来删除
2. 在最大优先级队列（max priority queue）中，当需要删除一个元素的时候，我们找到优先级最大的元素来删除

2. 最大优先级队列

2.1 ADT

AbstractDataType  MaxPriorityQueue
{
//有限的元素的结合，每个元素都有一个优先级
    Create(): create an empty priority queue //创建一个空的优先级队列
    Size():  return number of element in the queue //返回队列中元素的个数
    Max(): return element with maximum priority //返回队列中拥有最高优先级的元素
    Insert(x): insert x into queue //插入x进入队列
    DeleteMax(x):delete the element with largest priority from the queue; return it in x;//删除队列中最高优先级的元素，并且通过x返回它
}

实现：

1. 用无序线性表来进行实现
2. 插入元素到链表的最右边（时间复杂度为θ(1)）
3. 需要查找到最高优先级的元素并且删除这个元素（时间复杂度为θ(n)）

2.2 物理实现：Heap（堆）

2.2.1 Heap

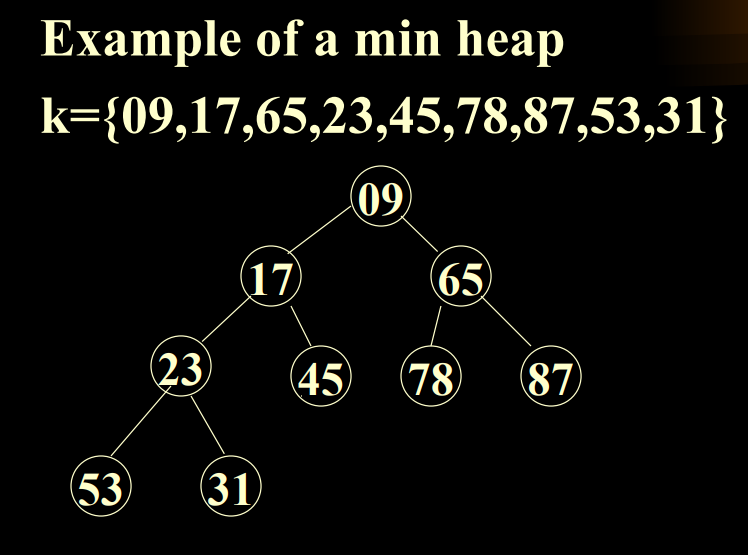
1. 堆中某个节点的值总是不大于或不小于其父节点的值（每一个节点上的值都大于(小于)或者等于他的子节点(如果有的话)）
2. 堆总是一棵完全二叉树

将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

2.2.2 实现

template<class T>class MaxHeap
{
    public:
        MaxHeap(int MaxHeapSize=10);
        ~MaxHeap(){delete[]heap;}
        int size()const{return CurrentSize;}
        T Max(){
            if (CurrentSize==0) throw OutOfBounds();
            return heap[1];
        }
        MaxHeap<T>&insert(const T&x); 
        MaxHeap<T>& DeleteMax(T& x);
        void initialize(T a[], int size,  int ArraySize);
    private:
        int CurrentSize, MaxSize;
        T * heap;
}

注：数组0号位置不用，也就是从Heap[1]开始使用

使用的堆是基于数组的，并没有创建一个真正的二叉树。

2.2.3 构造函数

template<class T> MaxHeap<T>::MaxHeap(int MaxHeapSize) {
    MaxSize=MaxHeapSize;
    Heap = new T[MaxSize+1];
    CurrentSize=0; 
}

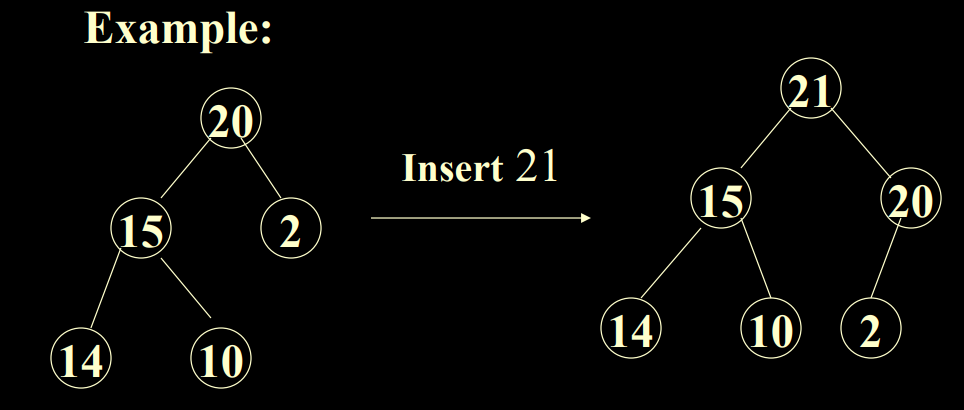
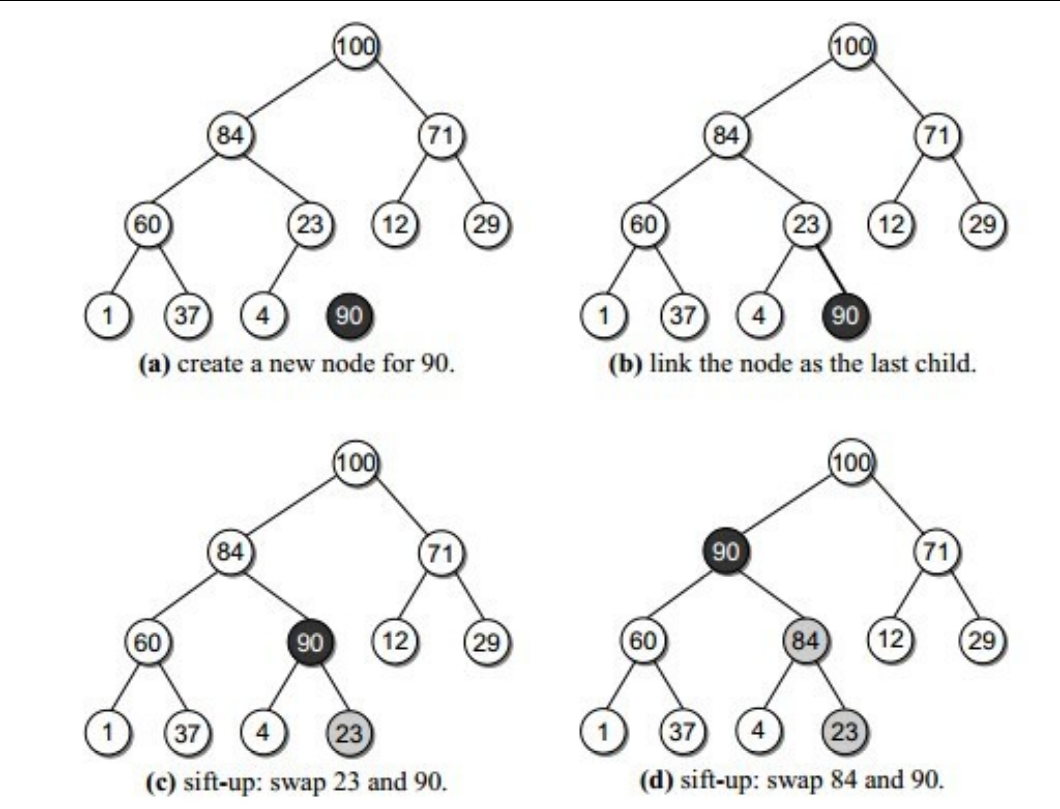
2.2.4 插入算法

在数组后面插入后，和其父结点进行比较，如果比父结点大，则交换，一直到不再大于其父结点

堆数组类似于下图：

template<class T>MaxHeap<T>& MaxHeap<T>:: Insert(const T& x){
    if(CurrentSize= =MaxSize) throw NoMem(); 
    int i=++CurrentSize;
    while(i!=1 && x>heap[i/2]){
        //0不使用
        heap[i]=heap[i/2];
        //不必每次都进行完全交换
        i/=2;
    }
    heap[i]=x;
    return *this;
}

时间复杂度：O(logn)

2.2.5 删除算法

只需要删除根（显而易见）

将根删除，将数组最后一个(最后一层最后一个元素)换为根，然后进行比较。

template<class T>MaxHeap<T>&  MaxHeap<T>:: DeleteMax(T& x){
    if(CurrentSize==0) throw OutOfBounds(); 
    x = heap[1];
    //0无存储，这个就是root结点
    T y=heap[CurrentSize--];//最后一个结点
    int i=1;//i标向树根
    ci=2;//ci先标到左子树
    while(ci<=CurrentSize){
        if(ci<CurrentSize && heap[ci]<heap[ci+1]){
            //如果ci未越界，并且左子树的值小于右子树的值。
            //找个大的和根换
            ci++;//转向右子树
        }
        if(y>=heap[ci]) break;
        heap[i]=heap[ci];
        i=ci;
        ci*=2;
    }
    heap[i]=y;//y是最后一个节点
    return *this;
}    

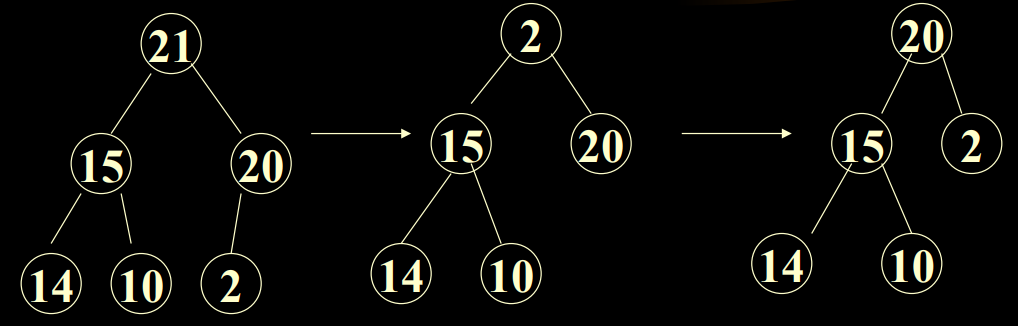
注：代码的做法，似乎和上图不一样。

代码的图：

​ 21 20 20

​ 15 20 ——> 15 20 ——> 15 20 ——> 15 2

14 10 2 14 10 2 14 10 2 14 10

时间复杂度：O(logn)

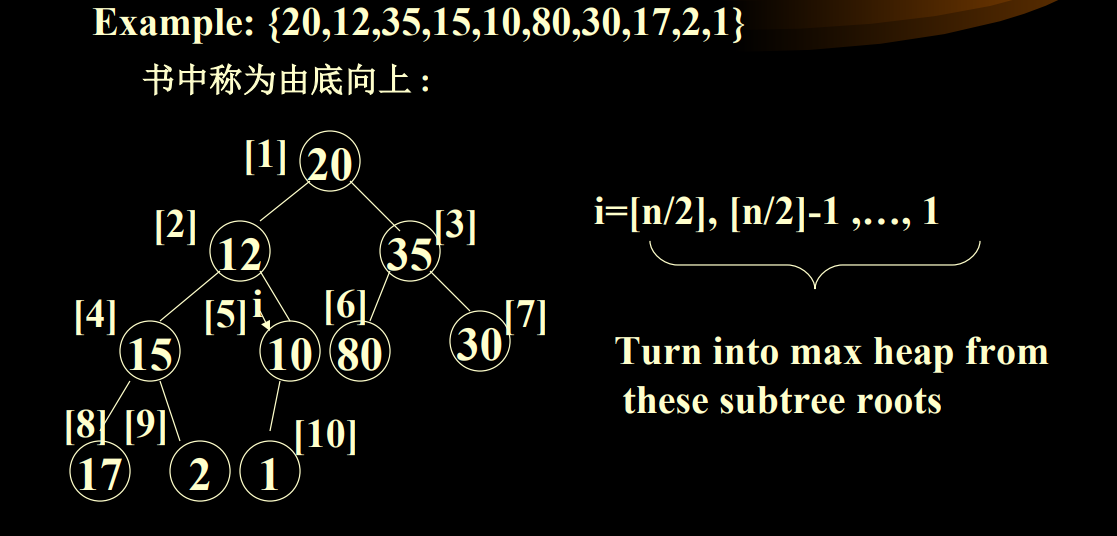
2.2.6 初始化一个非空的最大优先级数列

由底向上：

1. 把初始指针指向最后一个节点的父结点(N/2)，然后向前循环
2. 从最后一个节点的父结点开始（这样就可以保证所有非叶结点都可以操作到），对所有的非叶节点进行下滤操作

//C++
//注意是对每个子树进行递归处理
Template<class T> void MaxHeap<T>::Initialize (T a[],int size,int ArraySize) { 
    delete[] heap;
    heap=a;
    CurrentSize=Size;
    MaxSize=ArraySize;
    for( int i=CurrentSize/2; i>=1; i--) {
        T y=heap[i];
        //c为i的子树位置
        int c=2*i;
        while(c <= CurrentSize){
            //左右子树中找大的
            if(c<CurrentSize && heap[c]<heap[c+1])
                c = c+1;
            if(y>=heap[c])
                break;
            //根比子树小，就向下传动
            heap[c/2] = heap[c];
            c*=2;
            //找到其子节点位置
        }
        heap[c/2]=y;
    }
}

// java
private void buildHeap(){
    for( int i = currentSize / 2; i > 0 ; i-- )
        percolateDown(i);
}

复杂度分析：

“第i层交换的最大次数为k-i”的意思是“第i层的每一个元素交换的最大次数为k-i”

时间复杂度：O(n)

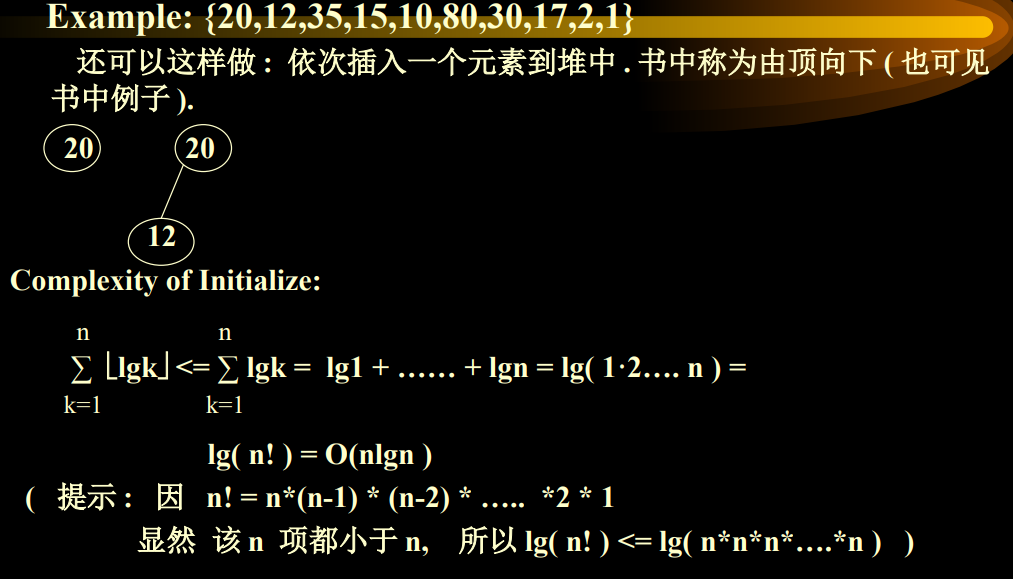
由顶向下：逐个做插入操作即可

时间复杂度：O(n logn)

3. 最小优先级队列

3.1 ADT

public class BinaryHeap {
    public BinaryHeap( )
    public BinaryHeap( int capacity )
    public void insert( Comparable x ) throws Overflow()
    public Comparable findMin( )
    public Comparable deleteMin( ) 
    
    public boolean isEmpty( )
    public boolean isFull( )
    public void makeEmpty( )
    
    private static final int DEFAULT_CAPACITY = 100
    private int currentSize
    private Comparable [ ] array;
    private void percolateDown( int hole ) 
    private void buildHeap( ) 
}
public BinaryHeap(){
    this( DEFAULT_CAPACITY );
}
public BinaryHeap( int capacity ) {  
    currentSize = 0;
    array = new Comparable[ capacity + 1 ];
}
public void makeEmpty( ) {
    currentSize = 0;
}

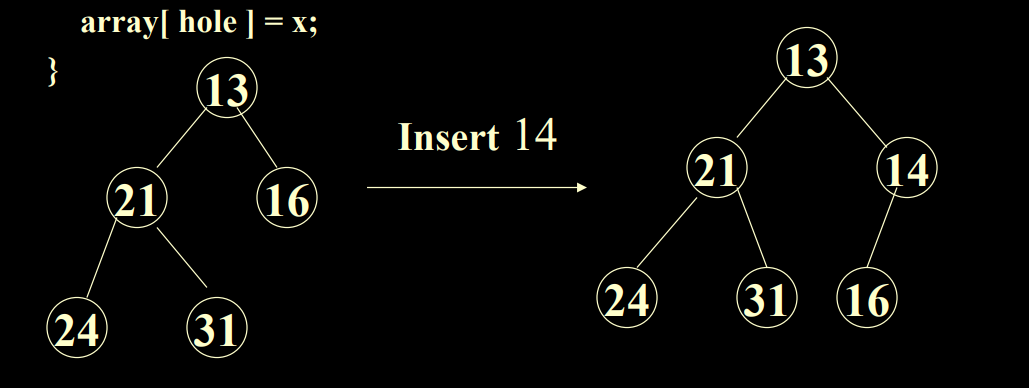
3.2 插入算法

//最小堆的插入算法
public void insert( Comparable x ) throws Overflow() {
    if(isFull()) throw new Overflow(); 
    int hole = ++currentSize;
    for(;hole>1 && x.comparebleTo(array[hole/2])<0;hole/= 2){
        array[hole] = array[hole / 2];
    }
    array[ hole ] = x; 
}

3.3 删除算法

public Comparable deleteMin(){
    if( isEmpty()) return null;
    Comparable minItem = findMin( );
    array[1] = array[currentSize--];
    percolateDown(1);
    return minItem;
}

//最小堆的，将hole下标的元素向下传动，下滤算法
private void percolateDown(int hole) {  
    int child;
    Comparable tmp = array[hole];
    for(;hole*2<=currentSize;hole = child) {
        child = hole * 2;//切入到左子树
        if(child!=currentSize && array[child+1 ].compareTo(array[child])<0)
            child++;//如果没有到头，并且右子树比左子树小，则转向右边的子树
        if(array[child].compareTo(tmp)<0)
            array[hole] = array[child];//如果小则进行交换 
        else
            break;
    }
    array[hole] = tmp;
} 

4. 应用

4.1 堆排序

1. 初始化一个n个元素的最大堆，O(n)

2. 每次我们删除最大的元素，调整堆的时间复杂度为O(log₂n)

3. 将待排序的序列构造成一个最大堆，此时序列的最大值为根节点
4. 依次将根节点与待排序序列的最后一个元素交换
5. 再维护从根节点到该元素的前一个节点为最大堆，如此往复，最终得到一个递增序列

时间复杂度：O(n) + O(nlogn)（每一个结点都会被删除，所以是n * logn） = O(n logn)

//c++
Template<class Type>void HeapSort(datalist<Type>&list){
    for(int i=(list.currentsize)/2;i>=1;i--) 
        FilterDown(i,list.currentsize);
    for(i=list.currentsize; i>1 ;i--){
        Swap(list.Vector[1],list.vector[i]); 
        FilterDown(1,i-1);
    }
}

//java
public static void heapsort( Comparable [] a ) {
    for( int i = a.length / 2; i >= 1; i-- ) 
        percDown( a, i, a.length );
    for( int i = a.length ; i > 1; i-- ) { 
        swapReferences(a,1,i);
        percDown(a,1,i-1);
    }
}
private static void percDown( Comparable [] a, int i, int n ) {
    int child;
    Comparable tmp;
    for( tmp = a[ i ]; leftChild( i ) < n; i = child ) {
        child = leftChild( i );
        if( child != n – 1 && a[child ].compareTo( a[ child + 1 ]) < 0 )
            child++;
        if( tmp.compareTo( a[ child ] ) < 0 )
            a[ i ] = a[ child ]; 
        else  break;
    }
    a[ i ] = tmp;
}
private static int leftChild( int i ) {  
    return 2 * i + 1;
}     

我认为根本不用这么烦，可以直接调用删除算法

5. 例题

答案：A