5.0 Hashing 哈希

1. 散列表 (Hash Table )

Address = hash(key)

设计目标：散列函数的复杂度理论上能够到达常数级别复杂度。

总体思路：给一个key，能找到value。那就需要有一个从key到地址的映射。

1. 桶（Bucket）： 桶是哈希表中的存储单元，通常是一个数组。每个桶可以存储一个或多个键值对。哈希表使用哈希函数将键映射到特定的桶。当发生哈希冲突时，即两个或更多键映射到同一个桶，解决冲突的方式可能包括使用链表、树等数据结构将多个键值对存储在同一个桶中。
2. 元素（Element）： 元素是指哈希表中存储的键值对。每个元素包含一个键和对应的值。元素被存储在桶中，通过哈希函数确定存储的桶的位置。在哈希表中，我们通常使用键来查找对应的值。

假设我们有一个存储学生信息的哈希表，其中键是学生的学号，值是学生的姓名。这个哈希表有10个桶（桶的数量通常是根据哈希表的大小确定的）。

哈希表： Bucket 0: [ ] Bucket 1: [ ] Bucket 2: [ ] Bucket 3: [ ] Bucket 4: [ ] Bucket 5: [ ] Bucket 6: [ ] Bucket 7: [ ] Bucket 8: [ ] Bucket 9: [ ]

并且我们使用以下哈希函数：hash(key) = key % 5

现在，考虑以下两个键值对发生了哈希冲突，它们都映射到了同一个桶：

1. 键: 3，值: “Alice”
2. 键: 8，值: “Bob”

键3和键8都映射到了桶3。

此时，桶3的状态可能是一个链表（或是一个数组，总之是线性表），如下所示：

Bucket 3: [ (3, “Alice”) -> (8, “Bob”) ]

在这个例子中，桶3中有两个元素，它们通过链表连接在一起。当需要查找键为3或8的值时，哈希表会在桶3的链表中进行线性搜索，直到找到相应的键值对。

这是一种简单的处理哈希冲突的方式。其他方法可能包括使用开放寻址法、二次探查等。

1.1 散列函数

1.1.1 如何寻找合适的散列函数

冲突选择合适的负载因子α=n/b

n：element的数量

b：bucket的数量

α > 1 碰撞频率大 α< 1 碰撞频率小

1.1.2 取余法

取最大质数：键可以被更均匀地分布到不同的桶中，减少了哈希冲突的概率。

1.1.3 平方取中法

1. 先进行原来的数据进行平方，然后选取中间的合适部分。
2. 对于一个值，按照某一进制下进行处理，处理后选择其中合适的中间部分。(类字符串进行存取)

1.1.4 乘法杂凑函数

%1是留下小数部分

例子中fai取了0.618

1.1.5 针对字符串-1

把字符串中的每一个字符的ASCII值或者Unicode值相加（再取模）

public static int hash( String Key, int tableSize ) {
    int hashVal = 0;
    for( int i = 0; i < Key.length( ); i++ )
        hashVal += Key.charAt( i );
    return hashVal % tableSize;
} 

TableSize = 10007, 如果所有key小于等于8个char, 8*127=1016，那hash函数只能有0-1016的结果，大大滴浪费。

字符串远远短于散列表的大小时，会导致浪费。

1.1.6 针对字符串-2

public static int hash( String key, int tableSize ){ // good hash fanction
    int hashVal = 0;
	for( int i = key.length( )-1; i > =0; i-- )
		hashVal = 37 * hashVal + key.charAt( i );
	hashVal %= tableSize;
	if( hashVal < 0 ) // 函数允许溢出，这可能会引进负数
	hashVal += tableSize;
	return hashVal;
}

对于每一个char，前面多一个系数。

1.2 如何解决散列表冲突问题

碰撞的两个(或多个)关键码称为同义词, 即H(k1) = H(k2), k1不等于k2

1.2.1 线性探测法（linear Probing）

如果key的哈希值是d，并且d对应的位置已经被占据，然后我们会按照线性顺序向后成环形查找

也就是向后塞

1. 例一：

   

平均成功访问次数：

1. 例二：

   

问题：堆积问题（clustering problem）：指不同的同义词表合为一张了。从而增加了插入，查找的时间。

这个方法也太二逼了

1.2.2 二次探测法(Quadratic probing)

如果H(k)已经被占据了，那就去以线性的顺序去找d + 1, d + 2², d + 3² ……

1.2.3 双散列哈希(Double Hashing)

第一个散列函数发生冲突，那么使用第二个散列函数来放置，如果再次冲突则进行相应探测。

如果k的第一哈希值为d，而这个对应的格子已经被占用，则我们继续计算k的第二哈希值，然后检查d+c，d+2c, d+3c…

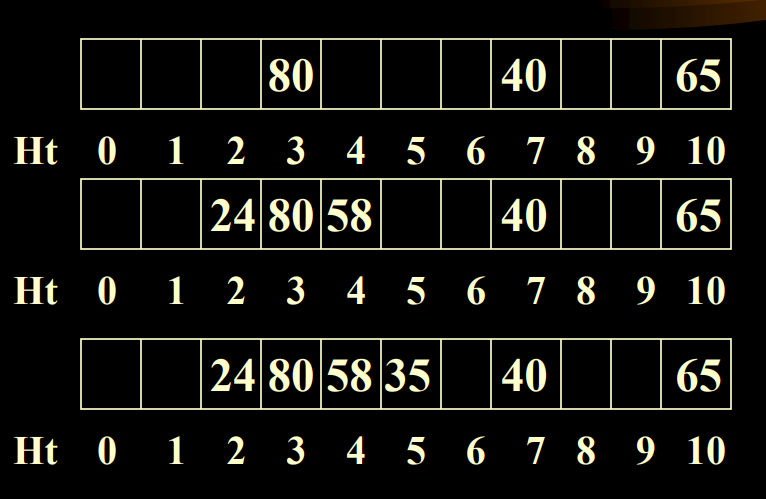
再散列(进行扩容)：当表项数 > 表的70% 时,可再散列。 即, 取比(2*原表长=14)大的质数17再散列。

6%17=6, 15%17=15, 23%17=6, 24%17=7, 13%17=13

（右边的键值有点乱，不用介意）

private void rehash(){
    HashEntry [] oldArray = array ;
    allocateArray(nextPrime(2*oldArray.length));
    currentSize = 0;
    for( int i = 0;i < oldArray.length;i++ )
        if(oldArray[i] != null && oldArray[i].isActive)
            insert(oldArray[i].Element);
}

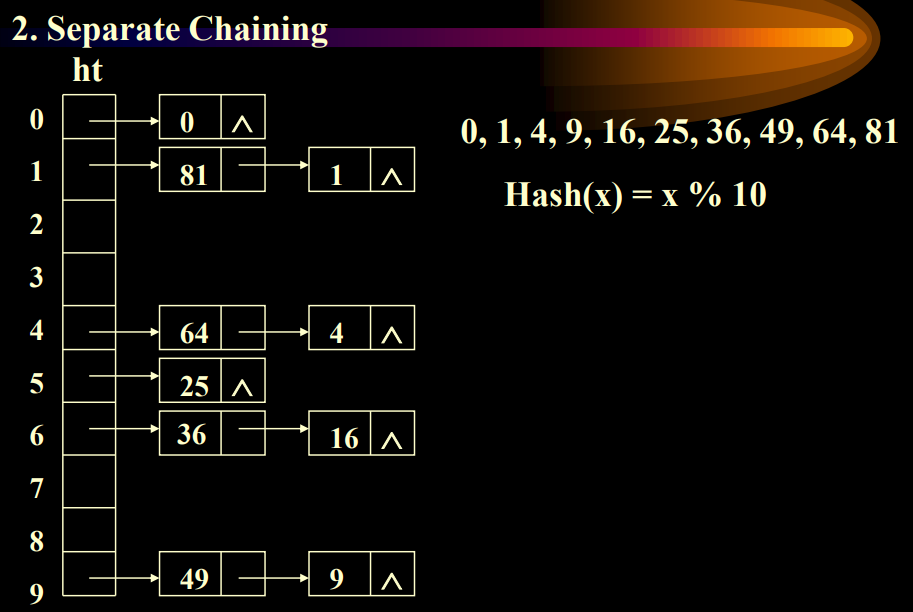
1.2.4 分离链接法(Separate Chaining)

使用每个位置对应线性表解决这个问题

避免了向后顺延。

1.4 实现

1.4.1 散列表的c++实现

1. 我们假设存储在散列表中的每一元素的类型是E，并且有一个类型为k的关键码
2. 散列表的实现使用了两个数组，一个是ht（也就是bucket），另一个是empty
3. ht[t]中含有element当且仅当empty[i]是true

template<class E,class K>
class HashTable{ 
    public:
        HashTable(int divisor =11);
        ~HashTable(){
            delete[]ht;
            delete []empty;
        }
        bool Search(const K&k ,E& e)const; 
        HashTable<E,K>&Insert(const E&e);
    private:
        int hSearch(const K& k)const;
        int D;//hash function divisor
        E *ht ; //hash table array
        bool *empty ; //1D array
};

1.4.2 线性探测法的c++实现

//hashtable的构造方法
template<class E,class K>//E和K需要被实例化后，这个类才能被调用。
HashTable<E,K>::HashTable(int divisor){
    D = divisor;
    ht = new E[D];
    empty= new bool[D];
    for(int i=0;i<D;i++)
        empty[i] = true;
}

template<class E,class K>
int HashTable<E,K>::hSearch(const K&k)const {
    int i= % D;//home bucket
    int j= i ; //start at home bucket
    do {
        if(empty[j] || ht[j]==k) return j;//fit
        j=(j+1)%D; //next bucket
    } while(j!= i);  //returned to home?是否循环完成一遍
    return j; //table full;
}

//参数进行引用K&k
template<class E,class K>
bool HashTable<E,K>::Search(const K&k,E&e)const{
    //put element that matches k in e.
    //return false if no match.
    int b= hSearch(k);
    if(empty[b]||Hash(ht[b])!=k)return false;
    e=ht[b];
    return true;
}

template<class E,class K>
HashTable<E,K>& HashTable<E,K>::Insert(const E& e) {
     K k=Hash(e);//extract key
     int b=hSearch(k);
     if(empty[b]){
        empty[b]=false;
        ht[b]=e;
        return *this;
    }
    throw NoMem();  //table full
}

1.4.3 二次探测法的java实现

public interface Hashable {
    int hash(int tableSize);
}
class HashEntry {
    Hashable element;
    boolean isActive;
    public HashEntry(Hashable e){this(e, true);
    }
    public HashEntry(Hashable e, boolean i) {
        this.element = e;
        this.isActive = i;
    }
}
public class QuadraticProbingHashTable {   
    public QuadraticProbingHashable()
    public QuadraticProbingHashable(int size)
    public void makeEmpty( )  
    
    public Hashable find(Hashable x)
    public void insert(Hashable x)
    public void remove(Hashable x)  
    
    public static int hash(String key, int tableSize)
    private static final int DEFAULT_TABLE_SIZE = 11;
    
    protected HashEntry [ ] array; private int currentSize;
    private void allocateArray(int arraySize )
    private boolean isActive( int currentPos )
    private int findPos( Hashable x )  
    private void rehash( )//需要扩大hash表大小的时候，再哈希
    private static int nextPrime( int n ) 
    private static boolean isPrime( int n )
}

//构造方法
public QuadraticProbingHashTable( ) {
    this( DEFAULT_TABLE_SIZE );
}
public QuadraticProbingHashTable( int size ) {
    allocateArray( size );
    makeEmpty( );
}
//其他方法
private void allocateArray(int arraySize){
    array = new HashEntry[arraySize];
}
//清空哈希表
public void makeEmpty() {
    currentSize = 0;
    for( int i = 0; i < array.length; i++ )
        array[ i ] = null;
}
//查找哈希表元素
public Hashable find(Hashable x) {
    int currentPos = findPos(x);
    return isActive(currentPos)?array[currentPos].element:null;
}
private int findPos(Hashable x) {
    int collisionNum = 0;
    int currentPos = x.hash(array.length); 
    while(array[currentPos] != null && !array[currentPos].element.equals(x)) {
        currentPos += 2*collisionNum – 1;//二次探测法 n2 - (n-1)2= 2n-1
        if(currentPos >= array.length)
            currentPos -= array.length;
    }//如果已经放满，并且要找的值不在里面会进入死循环
    return currentPos;
}
private boolean isActive( int currentPos )  {
    return array[currentPos]!=null && array[ currentPos ].isActive;
}
public void insert(Hashable x) {
    int currentPos = findPos(x);
    if(isActive(currentPos))
        return;
    array[currentPos] = new HashEntry( x, true );
    if( ++currentSize > array.length/2)
        rehash();
}
public final void remove(Hashable x) {  
    int currentPos = findPos(x);
    if(isActive(currentPos))
        array[currentPos].isActive = false;
}

1.4.4 分离连接法的java实现

public class SeparateChainingHashTable  {  
    public SeparateChainingHashTable( ) 
    public SeparateChainingHashTable( int size )
    public void insert( Hashable x )
    public void remove( Hashable x )
    public Hashable find( Hashable x )  
    public void makeEmpty( )
    public static int hash( String key, int tableSize )  
    
    private static final int DEFAULT_TABLE_SIZE = 101;
    private LinkedList [] theLists;
    private static int nextPrime( int n ) 
    private static boolean isPrime( int n ) 
}

public interface Hashable{
    int hash( int tableSize );
}
public class Employee implements Hashable { 
    public int hash( int tableSize ) { 
        return SeparateChainingHashTable.hash( name, tableSize );
    }
    public boolean equals( object rhs ) { 
        return name.equals( ( Employee) rhs ).name );
    }
    
    private String name;
    private double salary;
    private int seniority;
}

public SeparateChainingHashTable()  {
    this( DEFAULT_TABLE_SIZE );
}
public SeparateChainingHashTable(int size) {
    theLists = new LinkedList[ nextPrime( size ) ];
    for( int i = 0; i < theLists.length; i++ ) theLists[ i ] = new LinkedList( );
}
public void makeEmpty( )  {
    for( int i = 0; i < theLists.length; i++ )
    theLists[ i ].makeEmpty( );
}
public void remove( Hashable x ){
    theLists[ x.hash( theLists.length ) ].remove( x );
}
public Hashable find( Hashable x ) {
    return ( Hashable ) theLists[ x.hash( theLists.length ) ]. Find( x ). Retrieve( );
}
public void insert( Hashable x )  {  
    LinkedList whichList = theLists[ x.hash( theLists.length ) ];
    LinkedListItr itr = whichList.find( x );
    if( itr.isPastEnd( ) )
        whichList.insert( x, whichList.zeroth( ) );
}