文章

4.1 Specific Trees 搜索树

发表于
作者 Sa1i3ri 21 分钟阅读

1. Binary Search Trees 二叉搜索树

  1. 二叉搜索树是一个可以为空的二叉树。一个非空的二叉树都满足如下性质：

    1. 每一个元素都含有一个关键字，并且每一个元素都有独一无二的关键字
    2. 一个树的左子树的关键字小于根中的关键字
    3. 一个树的右子树的关键字大于根中的关键字
    4. 根的左右子树还是二叉搜索树

  2. 二叉搜索树需要满足的事情:在很大的数据量下，要能够很快的进行增删查改。这也就是二叉搜索树的优越性。

image-20231120084823998

1.1 Indexed Binary Search Tree 索引二叉搜索树

  • 索引二叉搜索树是从普通二叉搜索树衍生 而来的，方法是在每个树节点上添加字段 leftSize。
  • Leftsize 字段中的值=节点左侧子树的元素个数 +1

image-20231120085255271

image-20231120085351236

1.2 二叉搜索树的实现

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinaryNode {
    BinaryNode( Comparable theElement ) {
        this( theElement, null, null );//调用本类中的其他构造方法
    }
    BinaryNode( Comparable  theElement,  BinaryNode lt,BinaryNode rt ) {
        element = theElement
        left = lt;
        right = rt;
    }
    Comparable element;
    BinaryNode left;
    BinaryNode right;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

//二叉搜素树的实现
public class BinarySearchTree {
    public BinarySearchTree(){ root = null; }
    public void makeEmpty(){ root = null; }
    public boolean isEmpty(){ return root == null;}
    
    public Comparable find( Comparable x )
    {return elementAt( find( x, root));}
    public Comparable findMin()
    {return elementAt( findMin( root ) );}
    public Comparable findMax()
    {return elementAt( findMax( root ) );
    public void insert( Comparable x )
    {root = insert(  x, root );}
    public void remove( Comparable x ) {root = remove( x, root ); }
    public void printTree()//都是外部接口
    
    private BinaryNode root;
    private Comparable elementAt( BinaryNode t ){ return t == null ? Null : t.element; }
    private BinaryNode find( Comparable x, BinaryNode t )
    private BinaryNode findMin( BinaryNode t )
    private BinaryNode findMax( BinaryNode t )
    private BinaryNode insert( Comparable x, BinaryNode t )
    private BinaryNode remove( Comparable x, BinaryNode t )
    private BinaryNode removeMin( BinaryNode t )
    private void printTree( BinaryNode t )
}
//查找某个元素的算法
private BinaryNode find( Comparable x, BinaryNode t ) {
    if( t == null )
        return null;
    if( x.compareTo( t.element ) < 0 )
        return find( x, t.left );
    else if( x.compareTo( t.element ) > 0 )
        return find( x, t.right );
    else
        return t;//Match 
}
//查找值最小的结点
//使用递归查找结点
private BinaryNode findMin( BinaryNode t ) {  
    if( t == null )
        return null;
    else if( t.left == null )
        return t;
    return findMin( t.left );
}
//迭代找最小结点
private BinaryNode findMin(BinaryNode t){
    if(t != null){
        while(t.left != null){
            t = t.left;
        }
    }
    return t;
}
//递归找到最大结点
private BinaryNode findMax( BinaryNode t){
    if(t == null){
        return null;
    }else if(t.right == null){
        return t;
    }
    return findMax(t.right);
}
//迭代找到最大结点
private BinaryNode findMax( BinaryNode t ) { 
    if( t != null )
        while( t.right != null )
            t = t.right;
    return t;
}
//将数值插入固定位置的算法
private BinaryNode insert( Comparable x, BinaryNode t ) {
    //先查找一次，如果找到了就不用进行查找
    if( t == null )
        t = new BinaryNode( x, null, null );
    else if( x.compareTo( t.element ) < 0 )
        t.left = insert( x, t.left );
    else if( x.compareTo( t.element ) > 0 )
        t.right = insert( x, t.right );
    else ;//duplicate; do nothing
    return t;
}
//compareTo()方法如果小于返回负数，大于返回正数

插入示意图：

image-20231120090028892

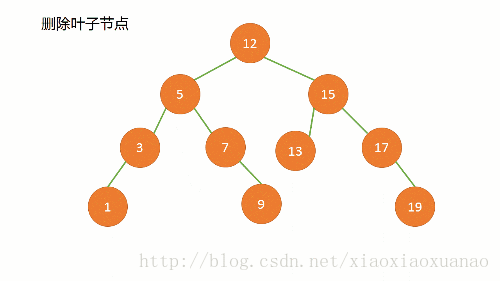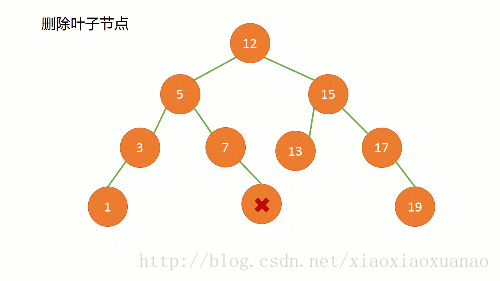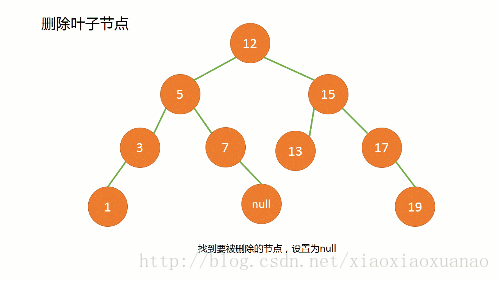
1.2.1 删除算法

  1. 如果结点本身不在树内，那么不需要删除

  2. 如果结点本身在树里面，删除需要分类

    1. 无子树:删除叶节点

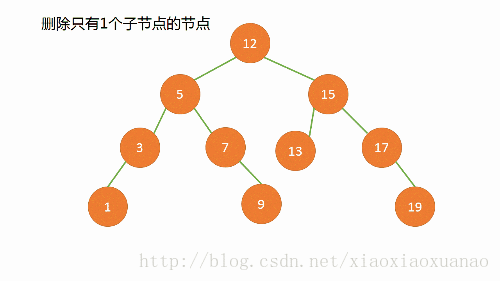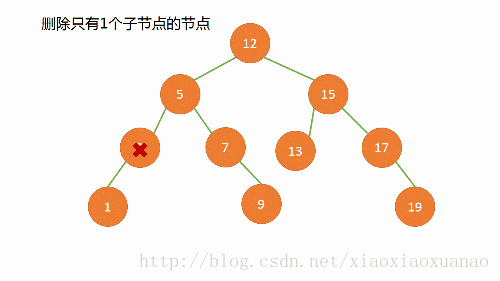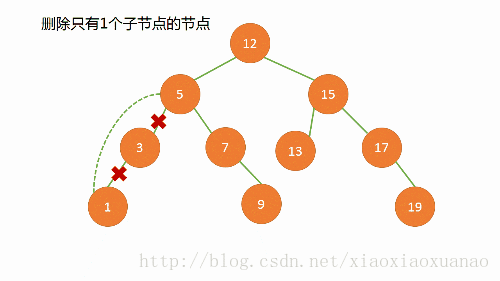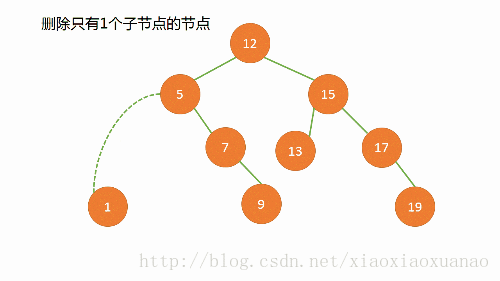
      这里写图片描述

    2. 一颗子树:直接连接

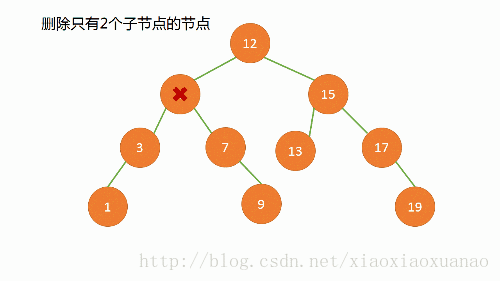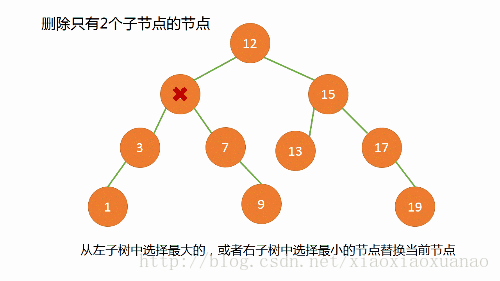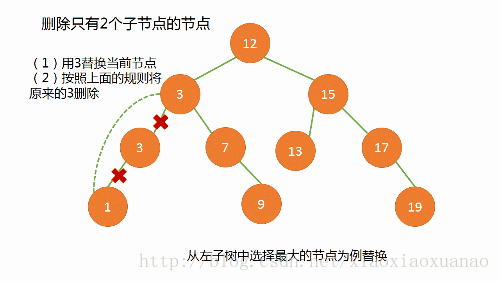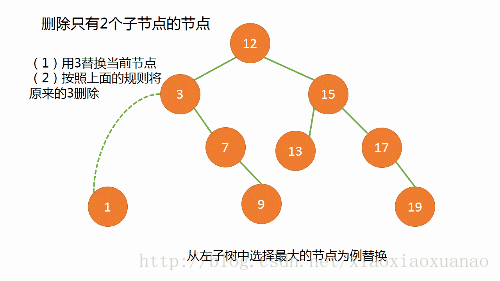
      这里写图片描述

    3. 两颗子树：找出左子树中最大或者右子树中最小的结点作为新结点

      这里写图片描述

      1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

      private BinaryNode remove( Comparable x, BinaryNode t ) {
    if( t == null )
        return t;
    if( x.compareTo( t.element ) < 0 )
        t.left = remove( x, t.left );
    else if( x.compareTo( t.element ) > 0 )
        t.right = remove( x, t.right );
    else if( t.left != null && t.right != null ) {
        t.element = findMin( t.right ).element;//把右树最小的复制给t
        t.right = remove( t.element , t.right );//递归的删除
    }else{
        t = ( t.left != null ) ? t.left : t.right;//一颗子树的情况
    }
    return t; 
}

1.3 高度

  1. 二叉搜索树的高度会直接影响搜索，插入和删除的时间复杂度。

  2. 最坏的情况就是把一个有序的数列添加进入到空的二叉搜索树中去。O(n)

    image-20231120092021274

  3. 最好的情况：O(log n)

    image-20231120092203815

2. AVL Tree 平衡二叉树

AVL树是一个用来增加二叉搜索树的所搜效率（通过增加平衡性）并且减小平均搜索高度。

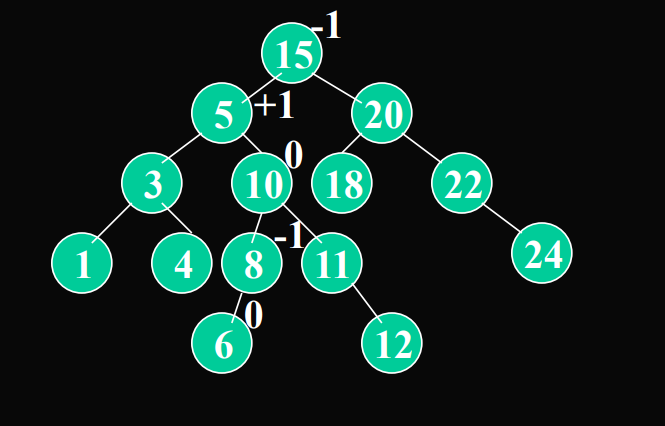
2.1 基本概念

  1. 定义：

    1. AVL树是一个二叉搜索树
    2. 对于每一个结点，其左子树和右子树的高度之差不超过1

  2. AVL树高：从根节点到每一个叶节点之间的所有路径的最长的一条

  3. 节点x的平衡因子 = x的右树的高度-x的左树的高度

    image-20231120092837033

    image-20231120093125960

  4. AVL的高度是O(log2n)的，所以搜索的算法复杂度也是O(log2n)。

2.2 插入

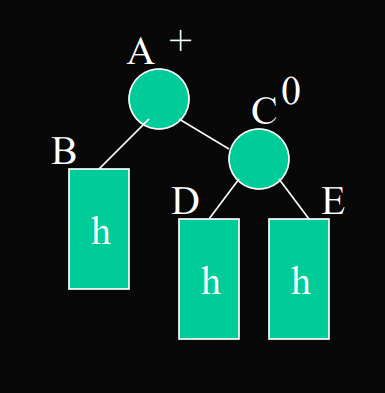
image-20231120135248736

  • 抽象得看，每个AVL树都大概可以看成这个样子

  1. 插入C的右子树 外侧加高(对A而言)

    image-20231120135858646

  2. 插入C的左子树 内侧加高（对A而言）

    image-20231120135951474

    调整后：树高不变。原h+2,插入后h+3,调整后h+2

  3. 调整只要在包含插入结点的最小不平衡（平衡因子>=2或<=-2）子树中进行

2.2.1 算法说明

如果没有失衡（没有结点的平衡因子的绝对值大于等于2），那就不需要旋转。

左旋和右旋只会涉及三个结点：失衡节点，失衡节点的某一子节点

左右双旋和右左双旋只会涉及三个结点：失衡节点，失衡节点的某一子节点，失衡节点子节点的某一子节点。

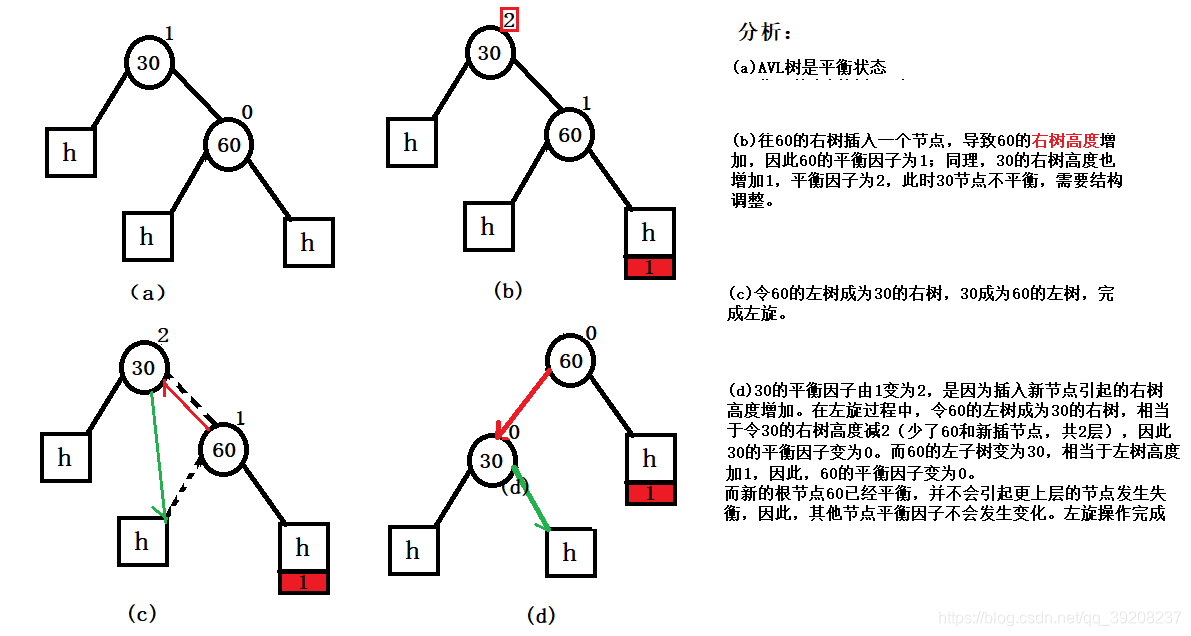
2.2.1.1 左旋

在这里插入图片描述

  1. 左旋的条件：

    从插入的结点一路向上找，找到的第一个失衡结点的平衡因子为2，该失衡节点向下的第一个子结点的平衡因子为1。

  2. 左旋的算法：（如上图）

    1. subL->right = ptr->left
    2. prt->left = subL
    3. ptr->bf = sub->bf = 0（调整平衡因子）

在这里插入图片描述

2.2.1.2 右旋

在这里插入图片描述

  1. 右旋的条件：

    从插入的结点一路向上找，找到的第一个失衡结点的平衡因子为-2，该失衡节点向下的第一个子结点的平衡因子为-1。

  2. 右旋的算法：（如上图）

    1. subR->left = ptr->right
    2. ptr->right = subR
    3. ptr->bf = subR->bf = 0

在这里插入图片描述

2.2.1.3 左右双旋

在这里插入图片描述

  1. 左右双旋的条件：
    1. 从插入的结点一路向上找，找到的第一个失衡结点的平衡因子为-2，该失衡节点向下的第一个子结点的平衡因子为1。
  2. 左右双旋的算法：（如上图）
    1. 对于那个平衡因子为1的结点，和它的子结点来一次左旋
    2. 对于那个失衡结点，与（1）中的子节点，来一次右旋
2.2.1.4 右左双旋

在这里插入图片描述

  1. 右左双旋的条件：
    1. 从插入的结点一路向上找，找到的第一个失衡结点的平衡因子为2，该失衡节点向下的第一个子结点的平衡因子为-1。
  2. 左右双旋的算法：（如上图）
    1. 对于那个平衡因子为1的结点，和它的子结点来一次右旋
    2. 对于那个失衡结点，与（1）中的子节点，来一次左旋

2.2.2 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

private AVLNode insert( Comparable x, AVLNode t ) {
    if (t == null)
        t = new AVLNode( x, null, null );
    else if ( x.compareTo(t.element) < 0 ){
        t.left = insert(x, t.left);//不仅x插入左子树，而其左子树已经调平衡了，也就会子树已经旋转过了
        if(height(t.left) – height(t.right) == 2 )
            if(x.compareTo(t.left.element)<0)
                //根据大小进行调整
                t = rotateWithLeftChild (t);//左子树的左子树，只要做一次左向单旋
            else t = doubleWithLeftChild(t);//左子树的右子树，需要做一次左右双旋
    //下面是对称的插入在右子树上
    }else if(x.compareTo(t.element)>0) { 
        t.right = insert(x, t.right );
        if( height(t.right)–height(t.left)== 2)
            if(x.compareTo(t.right.element)>0)
                t = rotateWithRightChild(t);
            else t = doubleWithRightChild(t)
    }else;
    t.height = max(height(t.left), height(t.right)) + 1;
    return t;
}

左旋：

image-20231120152420096

1
2
3
4
5
6
7
8

private static AVLNode rotateWithRightChild(AVLNode k2){
    AVLNode k1 = k2.right;//k1持有k2的右子树
    k2.right = k1.left;//k2的右子树挂到k1的左子树上
    k1.left = k2;//把k2自己挂到k1的左子树上
    k2.height = max(height(k2.left),height(k2.right)) + 1;
    k1.height = max(k2.height,k1.right) + 1;
    return k1;
}

右旋：

image-20231120152444520

1
2
3
4
5
6
7
8

private static AVLNode rotateWithLeftChild( AVLNode k2 ) {
    AVLNode k1 = k2.left;//k1持有k2的左子树
    k2.left = k1.right;//k1的右子树挂到k2的左子树上
    k1.right = k2;//把k2自己挂到k1的右子树上
    k2.height = max(height(k2.left), height(k2.right)) + 1 ;
    k1.height = max(height(k1.left), k2.height) + 1;
    return k1;
}

左右双旋：

image-20231120152513374

1
2
3
4

private  static AVLNode doubleWithLeftChild( AVLNode k3 ) {
    k3.left = rotateWithRightChild(k3.left);
    return rotateWithLeftChild( k3 );
}

右左双旋：

image-20231120152619104

1
2
3
4

private static AVLNode doubleWithRightChild(AVLNode k3){
    k3.right = rotateWithLeftChild(k3.right);
    return rotateWithRightChild( k3 );
}

2.3 删除

方法 ： 与二叉搜索树的删除方法一样。

image-20231120153105160

image-20231120153258218

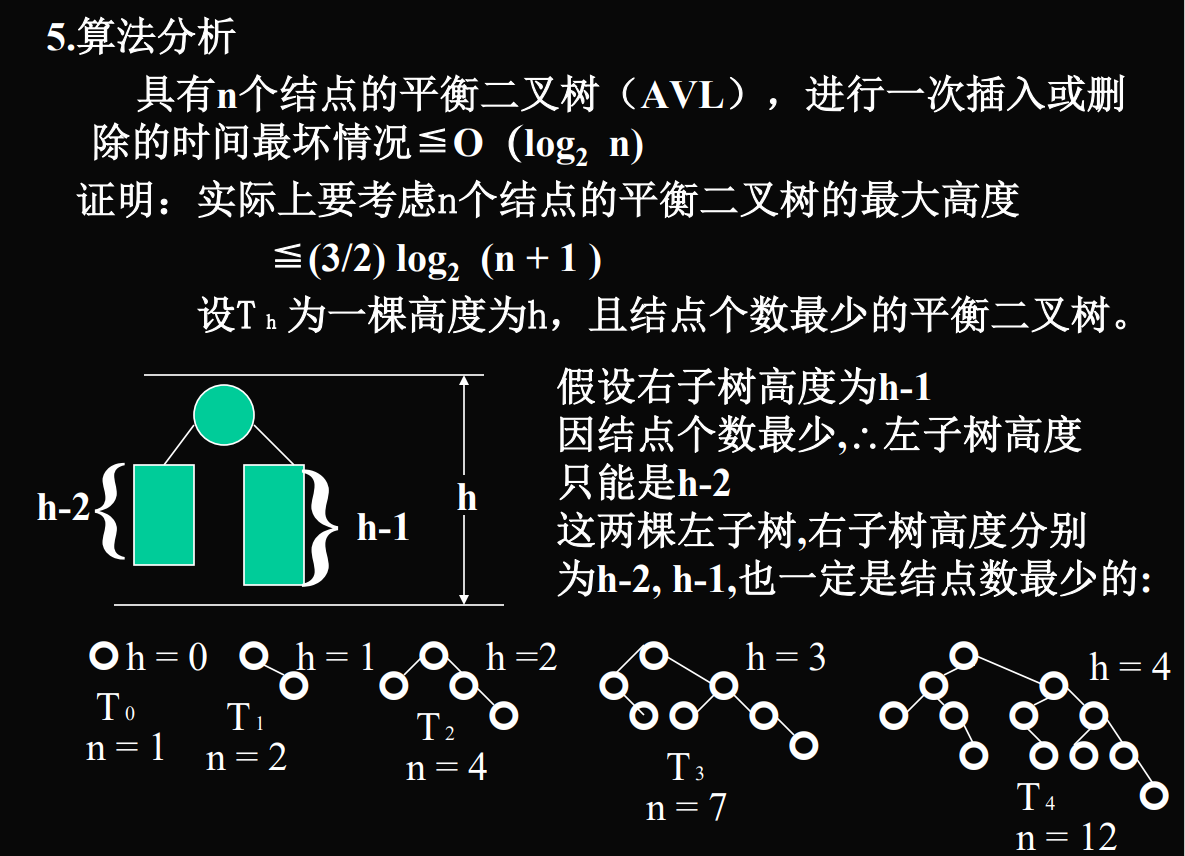
2.4 算法复杂度分析（不做要求）

具有n个结点的平衡二叉树（AVL），进行一次插入或删除的时间最坏情况<= O(log2 n)

image-20231120153610909

image-20231120153631941

image-20231120153707146

3. B-TREES

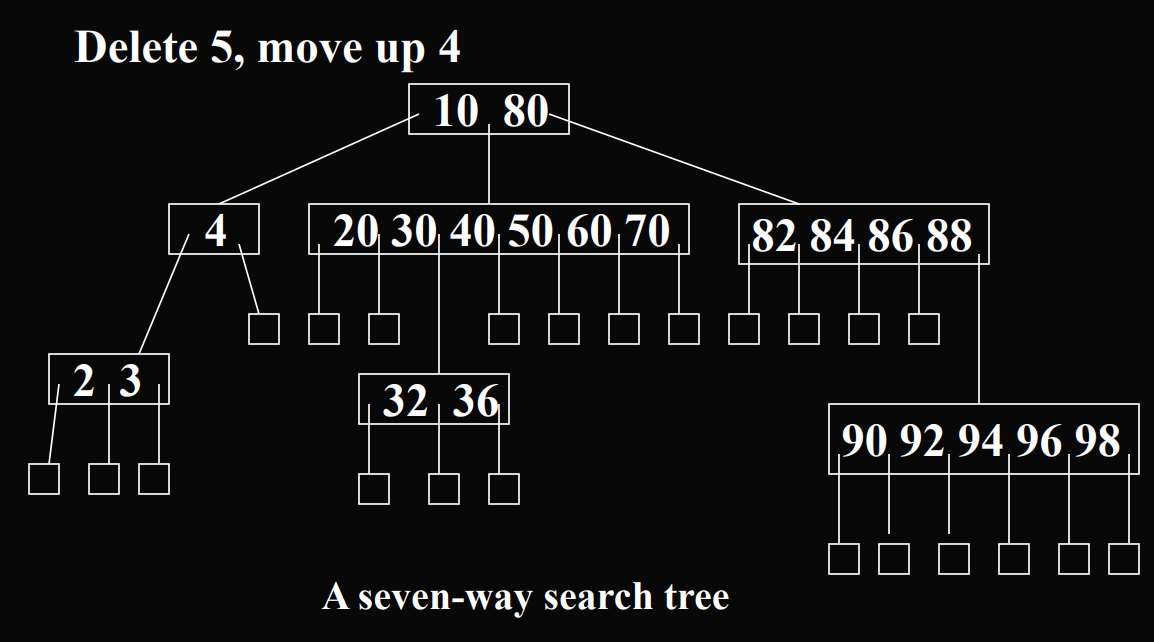
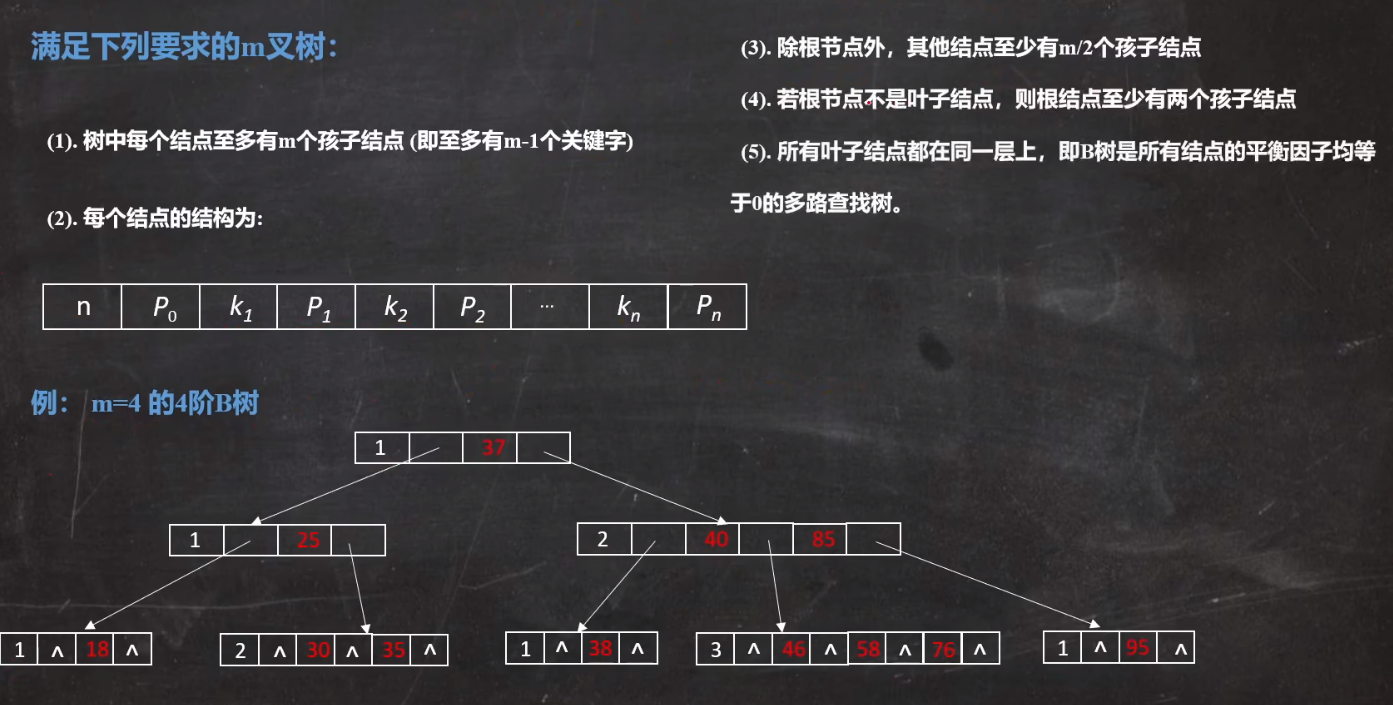
3.1 m叉搜索树

3.1.1 定义

  1. 搜索树可能为空。如果是一个非空的树，则为满足以下属性的树：
    1. 在相应的扩展搜索树(用外部节点替换零指针获得)中，每个内部节点最多有m个子节点，在1和m-1元素之间。
    2. 每个具有p元素的节点正好有p+1子节点。
    3. 每个结点这样构成：image-20231120155350389，k1 < k2 <……< kp，c0,c1…cp是p+1个子结点
  2. 对于在image-20231120155350389中的结点：
    1. ci ：在以Ci为根的所有子树中的结点的值都大于ki+1，小于ki。

image-20231120155907881

3.1.2 操作

3.1.2.1 插入
  1. 如果一层没有满，就在同一级进行插入。(针对的是m叉的情况)
  2. 如果这一层已经满了，那么在下一层进行插入。

image-20231120160125557

image-20231120160137407

3.1.2.2 删除

  1. 类型一：同一层还有节点，直接删除没有影响：

    image-20231120160324692

  2. 类型二：本层删除后没有节点，所以需要把底下能合适的最大(最小)的进行提升

    image-20231120160351278

3.1.2.3 m叉搜索树的行高
  1. 一个高为h的m路搜索树最少有h个结点(每一层只有一个结点)，最多有mh-1个结点
  2. logm(n+1) <= h <= n

3.2 平衡的m路搜索树——B树

3.2.1 定义

  1. m阶的B树是一个m叉搜索树。如果B树不为空，则B树有相应的扩展属性:
    1. 根结点至少有两个子女
    2. 所有非叶子结点的结点都至少有m/2(向上取整)个子结点
    3. 所有的叶子结点必须都在同一层
    4. 除根节点外，其它节点都包含 n 个key，其中 m/2（向上取整） -1 <= n <= m-1

image-20231120170436752

解释：这要从B树的生成开始说起。具体以一颗4阶树来展示B-tree的插入过程。

首先我们 插入 200，300，400，没有什么问题，直接插入就好。

200300400

现在我们接着插入500

200300400500

这个时候我们就需要分裂，将中间的key上移到父节点，左边的作为左节点，右边的作为右节点，如下图所示：

img

此时就可以相通性质2了，如果根节点不是叶子节点，那么它肯定发生了分裂，所以至少会有2个子节点。

同样我们接着插入600，700，800，900插入过程如下图所示：

img

现在根节点也已经满了，如果我们继续插入910，920，会怎样呢？根节点就会继续分裂，树继续向上生长。看下图：

img

通过整个的插入过程我们也会发现，B-tree和二叉树的一个显著的区别就是，B-tree是从下往上生长，而二叉树是从上往下生长的。

首先我们知道子节点的个数是等于key的数目+1，然后一个节点达到m个key后就会分裂，所以分裂后的节点最少能得到 m/2 - 1个key 。为啥还要减一呢？因为还要拿一个作为父节点。所以这个节点最少会拥有 m/2 - 1 + 1 = m/2 个子节点。

因为最少有m/2个子节点，所以最少就含有m/2-1个key，m 阶树，每个节点存到了m个key就会分裂，所以最多就有 m-1个key。

3.2.2 性质

  1. 所有的叶子结点都有相同的层数
  2. 叶子节点的个数等于关键字个数+1

3.2.3 搜索算法

B树的搜索算法和m叉搜索树的搜索算法是一样的。

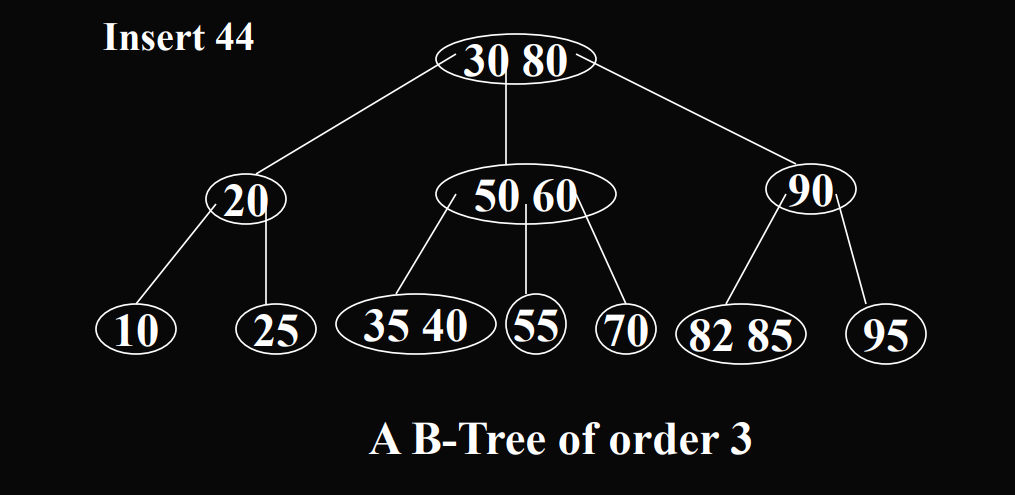
3.2.4 插入算法

B树的插入问题经常发生在叶子结点的上一层

思想：

  1. 做插入的时候优先插入叶节点:

    1. 如果叶节点还没有满的时候，直接插入即可
    2. 如果叶节点已经满了的时候，会进行分类，将中间节点的一个值拉到上级结点(这个结点在中间)。

    image-20231120172020093

  2. 插入到一个有满子结点的节点中，比如25插入上面那个例子中，满了的节点会分裂成两个节点,就是把中间的提升，将剩下的裂开

    image-20231120172042768

    image-20231120172353543

3.2.5 删除算法

  1. 首先判断删除的关键码是否都在B树中，不在的话直接退出。

  2. 判断本结点的key数量是否大于m/2（向上取整） -1，如果是直接删除这个key

  3. 如果本结点的key数量小于等于m/2（向上取整） -1

    1. 兄弟结点的key数量大于m/2（向上取整） -1，从父节点中要一个key，然后由兄弟节点补一个key到父节点
    2. 如果兄弟结点的key数量小于等于m/2（向上取整） -1
      1. 如果父节点的key数量大于m/2（向上取整） -1，从父节点要一个下来，然后兄弟合并即可
      2. 如果父节点的key数量小于等于m/2（向上取整） -1，先从父节点要一个key，然后以父节点为新的当前节点递归。如果到根结点都不能满足其他条件，只能将树的高度-1.

    e.g.

    img

    1. 删除80

      img

      删除200，那么我们先找到后继key 230，将后继key的值赋给它，然后我们需要删除的就是后继key 230 这和上面的情况就一样了

      img

    2. 删除180，将父节点中的 230 要下来，然后兄弟节点在补一个 240 到父节点

      img

    3. 删掉 50，父节点向上递归

      img

    4. 删除 140，从父节点直接要一个过来

      img

3.2.6 B树的结构

image-20231121081749224

  1. S是节点的元素的个数
  2. ei</sub是key，按照键值升序排列
  3. Ci是子树结点
大二上, 数据结构与算法
课内笔记 大二上 数据结构与算法
本文由作者按照 CC BY 4.0 进行授权