4.0 Tree

发表于 2023/11/14 更新于 2023/11/16

作者 Sa1i3ri 27 分钟阅读

1.Tree 树

定义：树T是结点的集合
这个集合可能为空，否则这个树是由一个特殊的根节点和0个或多个子树组成

1.1 术语

Degree of an elements(node) 结点的度数:有多少个子节点
Degree of a tree 树的度:树里面结点的最大的度数。
Leaf 叶结点:树里面度数为0的节点。
Branch 分支结点:树里面度数不为0的节点。
Level 层:各结点的层次为0或1，结点的层次等于其父结点的层次+1
Depth(Height) of a tree 树的高度:所有结点的最大层次数。

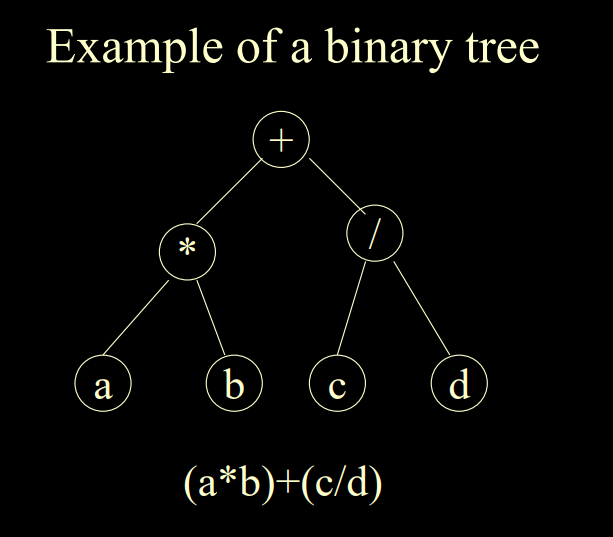
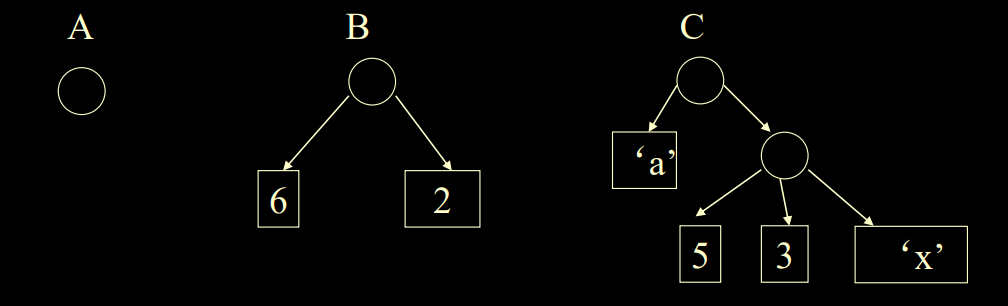
2.Binary Trees 二叉树

定义：二叉树 t 是一个有限的结点的集合（每一个结点的度都小于等于2）
特点：
1. 每个结点都有且只有两个子树（子树可能为空）
2. 每个结点的两个子树是有区别的，要区分出左子树和右子树

（此图高度为2）

2.1 二叉树的性质（考前重点）

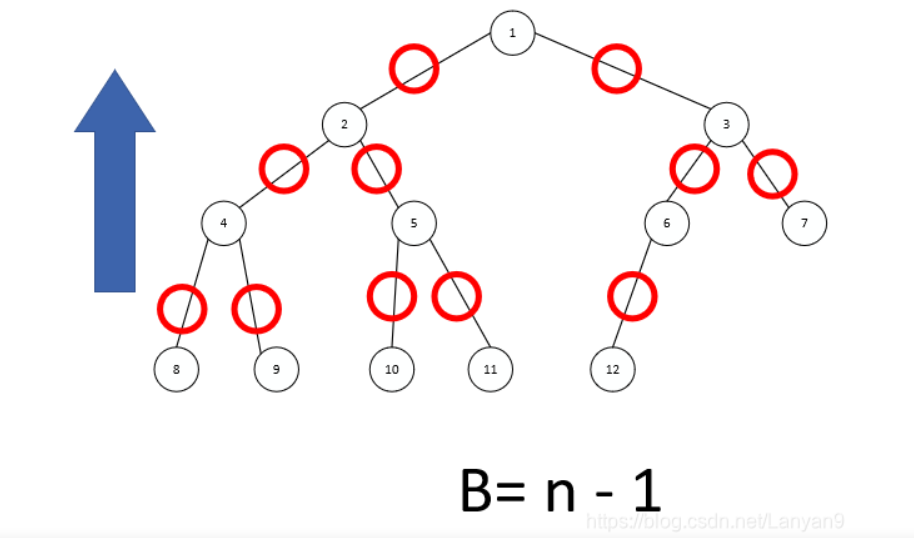
一共n个结点的二叉树有n-1条边。
第i层的结点数最多是2ⁱ个
高度为h(从0开始计)的二叉树中结点最少h+1个，最多2^h+1-1
如果一颗二叉树有n₀个树叶，并且结点度数为2的节点有n₂个，则n₀=n₂+1个
- 从下往上思考，可以看做是每个节点都有一个边与之对应，那么可以有B = n - 1成立，之所以有减一是因为根节点没有边与之相连（B为边数）
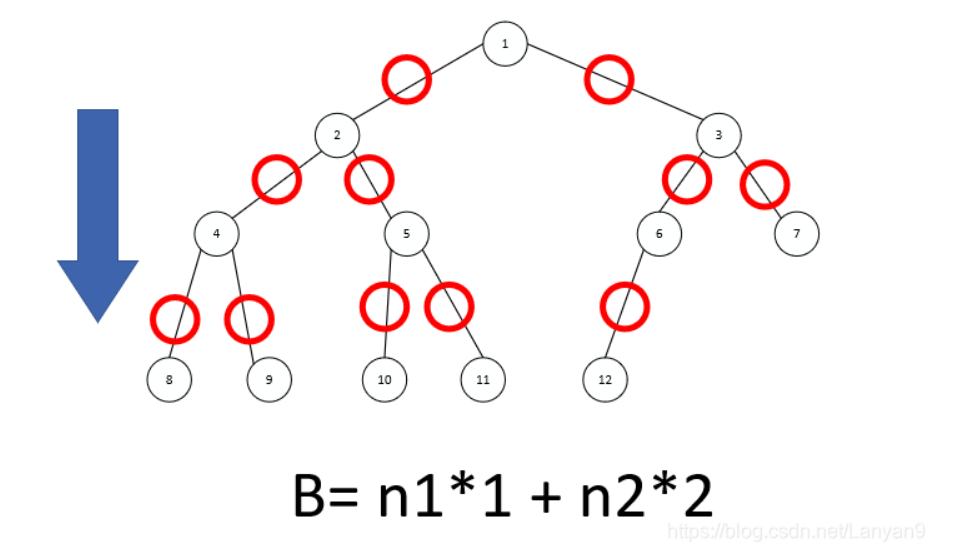
- 从上往下考虑，那么边的总数就等于度为1的节点乘1，度为2的节点乘2，依次类推，所以这里有B = n1 * 1 + n2 * 2
- 联立两个式子：n0 = n2 + 1
- 注意这里不失一般性：结点数、度数、叶子数可以相互转换
  在一棵度为4的树T中，若有20个度为4的节点，10个度为3的节点，1个度为2的节点，10个度为1的节点，则树T的叶节点个数是？
  20 * 4 + 10 * 3 + 1 * 2 + 10 * 1 = 20+10+1+10+n0 - 1
有n个结点的二叉树的高度最大为n-1，最小为log₂(n+1)(向上取整)-1

2.2 full binary tree 满二叉树

定义：将二叉树排满，也就是如果高度为n的树，其节点数为2ⁿ⁺¹-1个

2.3 complete binary tree 完全二叉树

定义：设二叉树的深度为h
1. 除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数(即1~h-1层为一个满二叉树)
2. 第 h 层所有的结点都连续集中在最左边。
ppt里的定义（~~异言丁真，鉴定为：不说人话~~）：
1. 假设我们为一个高度为h的满二叉树进行使用0 - 2^h+1的数字进行编码（这里ppt中是错误的，以我为准）
2. 我们从0层到h层，从上到下，从左到右，进行编码
3. 删除 k 个编号为（2h+1 -i）的结点, （1<=i<=k），得到的就是完全二叉树。
性质六: 假设i,0<=i<=n-1，是一个完全二叉树的一个节点的编号
- 1) 如果i=0，则是根节点，不然其父结点的编号为 (i-1)/2(向下取整)
- 2) 如果2*i+1>=n，那么这个元素没有左子女，不然左子女的编号就是这个数字
- 3) 如果2*i+2>=n，那么这个元素没有右子女，不然右子女的编号就是这个数字

2.4 二叉树的物理实现

2.4.1 数组

~~让数组搞这玩意属实有点为难了~~

普通的二叉树被视为缺失一些元素的满二叉树

很稀疏的二叉树会导致数组存储二叉树有大量的内存空间被浪费掉。

2.4.2 链表

Linked representation，也被称为L-R链表存储。

游标(Cursor)表示法：

结点代码

  
class BinaryNode {
    BinaryNode(){Left=Right=nullptr;}
    BinaryNode(Object e)
        {element=e; Left=Right=nullptr;}
    BinaryNode(Object e,  BinaryNode l, BinaryNode r)
        {element=e;  Left=l;  Right=r; }
    Object element;//存的数据
    BinaryNode left;//左子树
    BinaryNode right;//右子树
};

ADT

Create() 

IsEmpty() 

Root(x) 

MakeTree(root, left, right)

BreakTree(root, left, right) 

PreOrder()：以前序输出data

InOrder()：以中序输出data

PostOrder()：以后序输出data

LevelOrder()：以广度优先输出data

Delete():删掉一个二叉树，并且free掉所有结点

Height():返回树的高度

Size():返回树的结点数量

  
//计算二叉树的高度
//树的高度这么算：max{hl, hr}+1
template<class T> int BinaryTree<T>::Height(BinaryNode<T> *t)const {
    if(!t) return 0;
    int hl=Height(t->Left);
    int hr=Height(t->Right);
    //选择高的一颗树，将其高度增加
    if(hl>hr) return ++ hl;
    else return ++hr; }

二叉树代码

  
template<class T>class BinaryTree {
    public:
        BinaryTree(){root=0;};
        ~BinaryTree(){};
        bool IsEmpty()const
            {return ((root)?false:true);}
        bool Root(T& x)const;
        void MakeTree(const T& data, BinaryTree<T>& leftch, BinaryTree<T>& rightch);
        void BreakTree(T& data , BinaryTree<T>& leftch, BinaryTree<T>& rightch);
        void PreOrder(void(*visit)(BinaryNode<T>*u)) {PreOrder(visit, root);}
        void InOrder(void(*visit)(BinaryNode<T>*u)) {InOrder(visit, root);}
        void PostOrder (void(*visit)(BinaryNode<T>*u)) {PostOrder(visit, root);}
        void LevelOrder (void(*visit)(BinaryNode<T> *u));
    private:
        BinaryNode<T>* root;
        void PreOrder(void(*visit)(BinaryNode<T> *u),    BinaryNode<T>*t);
        void InOrder(void(*visit)(BinaryNode<T> *u),   BinaryNode<T>*t);
        void PostOrder(void(*visit) (BinaryNode<T> *u),  BinaryNode<T>*t);
};

部分实现细节：

  
template<class T>
void BinaryTree<T>::MakeTree(const T& data, BinaryTree<T>& leftch,BinaryTree<T>& rightch){
    root=new BinaryNode<T>(data, leftch.root, rightch.root);//新树的root承接左右两子树的root
    leftch.root = rightch.root=0;//左子树和右子树不再有自己的root
}
template<class T>
void BinaryTree<T>::BreakTree(T& data, BinaryTree<T>& leftch,BinaryTree<T>& rightch)
{
    if(!root) throw BadInput();//树是空的
    data=root.element;
    leftch.root=root.Left; rightch.root=root.Right;//左子树和右子树重新有自己的root
    delete root;
    root=0;
}

2.5 二叉树的遍历

V—–表示访问当前结点

L——表示访问V的左子树

R——表示访问V的右子树

所以一共有6种顺序： VLR LVR LRV VRL RVL RLV

广度优先遍历（ Breath-First-Search，BFS）：从上到下一层一层遍历
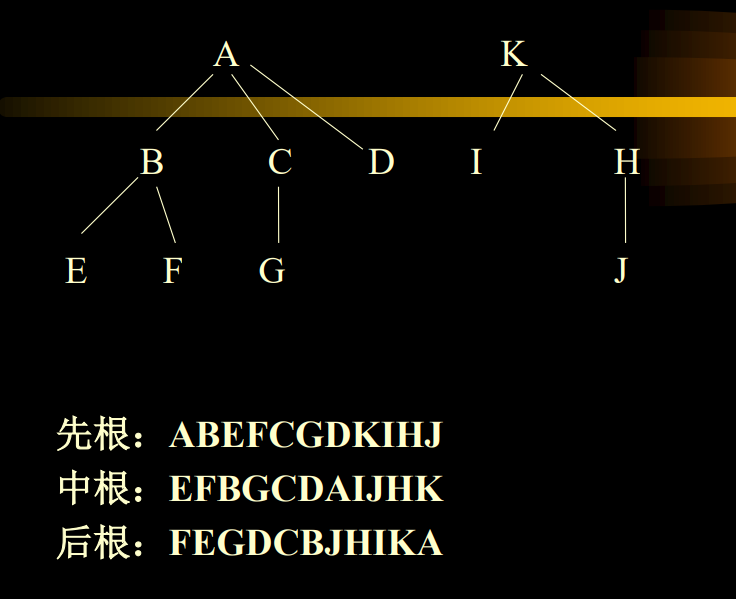
A B C D E F G
深度优先遍历（Depth-First-Search，DFS）沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点：
A B D E C F G
1. 先序遍历（Preorder）：VLR
2. 中序遍历（Inorder）：LVR
3. 后序遍历（Postorder）：LRV

2.5.1 广度优先遍历（BFS）

下面的代码不是ppt中的，ppt中的代码我认为是错误的。

  
void levelOrder() {
    std::queue<Node *> q;
    q.push(root);
    while (!q.empty()) {
        Node *node = q.front();
        q.pop();
        std::cout << node->key << " ";
        if (node->left)
            q.push(node->left);
        if (node->right)
            q.push(node->right);
    }

2.5.2 深度优先遍历（DFS）

二叉树的深度优先遍历，就是二叉树的先序中序后序。

普通树的深度优先遍历，先根次序遍历的结果，和其对应的二叉树的先序一致

普通树的深度优先遍历，后根次序遍历的结果，和其对应的二叉树的中序一致（因为一颗普通树转化为二叉树后，是没有右子树的）（为什么？见2.6.5）

2.5.2.1先序遍历

VLR

  
//递归实现先序遍历
void PreOrder(BinaryNode<T>* t) {
    if(t){
        visit(t);
        PreOrder(t->Left);
        PreOrder(t->Right);
    }
}

2.5.2.2中序遍历

LVR

  
//递归实现中序遍历
void InOrder(BinaryNode<T>* t) {
    if(t){
        InOrder(t->Left);
        visit(t);
        InOrder(t->Right);
    }
}

  
//非递归使用stack实现中序遍历
void Inorder(BinaryNode <T>*t){  
    Stack<BinaryNode<T>*> s(10);
    BinaryNode<T>*p = t;
    for (;;){
        //无条件进行循环
        while(p!=NULL){
            //一直进行压栈，直到最左下部分
            s.push(p);
            p = p->Left;
        }
        if(!s.IsEmpty()){
            //出栈输出，然后指向右子树，之后重复上面计算到右子树的最左边的节点。
            p = s.pop();
            visit(p);
            p = p->Right;
        }else
            return;
    }
}

2.5.2.3后序遍历

LRV

  
//递归实现后序遍历
void InOrder(BinaryNode<T>* t) {
    if(t){
        InOrder(t->Left);
        InOrder(t->Right);
        visit(t);
    }
}

  
//非递归实现后序遍历
//结点的实现
struct StkNode {
    BinaryNode <T> * ptr;
    int tag;//用来标记是否标记过了，第一次进栈为1，第二次进栈为2.
}
//非递归实现后序遍历
void Postorder(BinaryNode <T> * t) {
    Stack <StkNode<T>> s(10);
    StkNode<T> Cnode;
    BinaryNode<T>*p = t;
    for(;;) {
        //优先访问到最左下
        while (p!=NULL){
            Cnode.ptr = p;
            Cnode.tag = 0;
            s.push(Cnode);
            p = p->Left;
        }
        //将最左下结点出栈
        Cnode = s.pop();
        p = Cnode.ptr;
        while (Cnode.tag == 1)//从右子树回来 
        {
            //如果已经被访问一次了才进行输出
            cout << p->element;
            if (!s.IsEmpty()){
                Cnode = s.pop();
                p = Cnode.ptr;
            }else{
                //访问结束
                return;
            }   
        }
        Cnode.tag = 1;//从左子树遍历完，而右子树还没有动。
        s.push(Cnode);
        p = p->Right;//从左子树回来
    }
}      

2.6 二叉树的建立

2.6.1调用MakeTree函数

2.6.2 利用先序、中序唯一的构造一棵二叉树（精讲）

~~在这里ppt上竟然TMD把字符串从头到尾介绍了一遍，我觉得太脑残了就跳过吧~~

有先序、中序，可以唯一确定一棵二叉树。

先序遍历的第一个一定是树根，然后在中序遍历中找树根

然后在中序中树根左边是左子树，右边是右子树。与此同时，中序中树根的下标，正好是先序的左子树的最后一个结点的下标。

  
//是一个递归算法
BinaryNode<Type>*void CreateBT (String pres, ins) {
    int inpos;
    BinaryNode <Type>* temp;//当前二叉树的节点
    String prestemp, instemp;
    if (pres.length()==0) return NULL;
    else {
        temp = new BinaryNode; 
        temp->element=pres.ch[0];
        inpos=0;
        //从中序遍历中找到根节点的位置，这样子根节点左侧的是左子树，右侧的是右子树
        while (ins.ch[inpos]!=temp->element) 
            inpos++;
        
        //中序中树根的下标，正好是先序的左子树的最后一个结点的下标。
        prestemp = pres(1,inpos);//小括号是重载的，将先序遍历字符串的1到inpos取出来，赋给中间变量
        instemp= ins(0,inpos-1);
        temp->left = CreateBT(prestemp, instemp);
        
        prestemp=pres(inpos+1, pres.length()-1);
        instemp=ins(inpos+1, pres.length()-1);
        temp->right = CreateBT(prestemp, instemp);
        return temp;//完成组装返回
    } 
}

2.6.3 利用中序、后序唯一的构造一棵二叉树

先序遍历的树根在头部，而后序遍历串的树根在尾部，剩下的就和先序中序一样就行。

2.6.4 利用先序、后序构造一棵二叉树

不能做到唯一构造。

先序遍历串的第二个位置是左子树(左右子树分界点)，然后我们和后序遍历串结合。

考虑 AB BA。则A是树根，但是B在左还是右都可以，所以需要规定一下才能做到唯一构造。

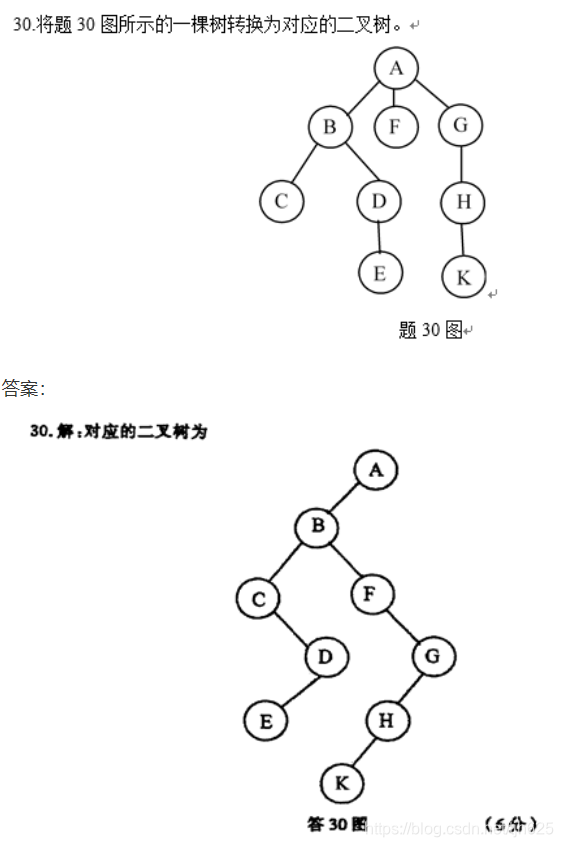
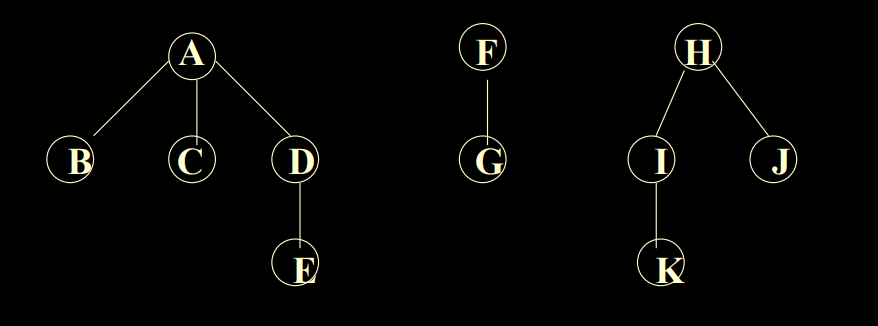
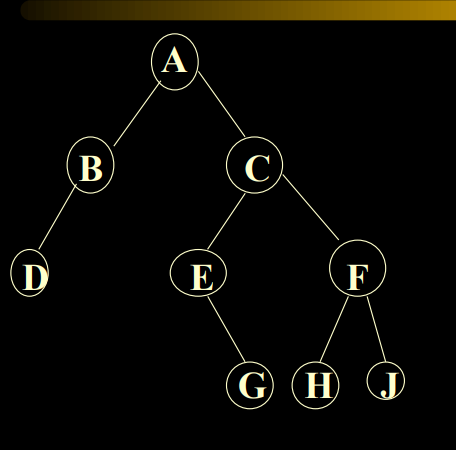
2.6.5 普通树转化为二叉树（个人补充）

将节点的孩子放在左子树
将节点的兄弟放在右子树

当然也可以这么理解：

在所有兄弟结点之间加一连线
对每个结点，除了保留与其长子的连线外，去掉该结点与其它孩子的连线

所以，转化后的二叉树，是没有右子树的。

2.7 树的表示方法

2.7.1 广义表（似乎不要求掌握太多）

a(b(f,g),c,d(h,i,j),e)

定义
定义为n(n>=0)个表元素a0,a1,a2,……an-1组成的有限序列, 记作: LS=(a0,a1,a2,……an-1)
- 其中每个表元素ai可以是原子,也可以是子表.
- 原子: 某种类型的对象,在结构上不可分(用小写字母表示).
- 子表: 有结构的。(用大写字母表示)
e.g：L = (3,(),(b,c),(((d))))
基础概念
1. 广义表的长度:表中元素的个数
2. 广义表的表头(head),表尾(tail)
  - head=a0
  - tail=(a1 , a2 ,……an-1 )
3. 广义表的深度: 表中所含括号的最大层数
性质
1. 有序性
2. 有长度,有深度
3. 可递归,如：F=(4, F)
4. 可共享,如：E=(B, D)，D=(B, C, A)，E中B为E,D所共享
5. 各种广义表都可用一种示意图来表示,用圆表示表元素, 用长方形表示原子
实现
放个思路，剩下的大家自己看吧

2.7.2 双亲表示法

记下自己的父结点位置，问题是:找子节点需要遍历一遍。

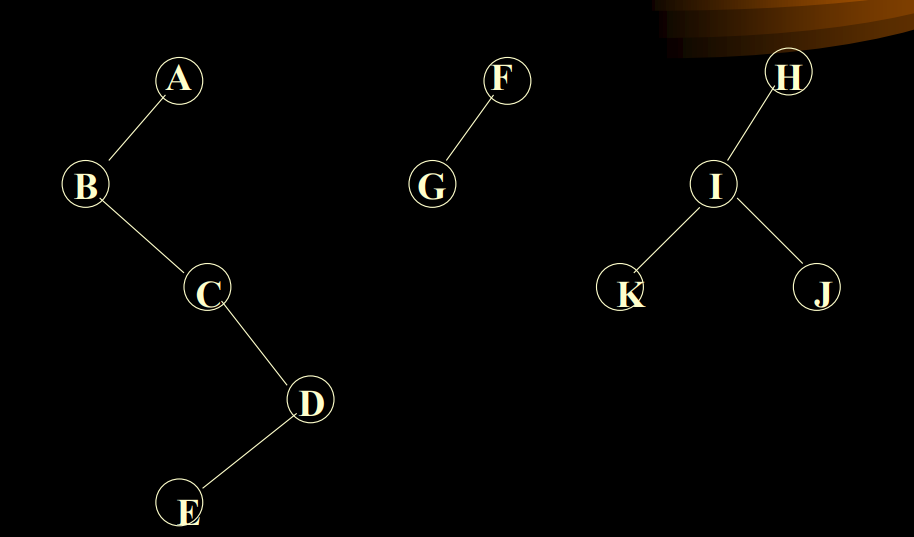
2.7.3 左子女—右兄弟表示法

就是把一颗树变成二叉树（通过2.6.5），然后再存储。

  
//左子女——右兄弟表示法
class TreeNode:
    T data;
    TreeNode *firstchild, *nextsibling;

class Tree:
    TreeNode * root,  *current;

template <class T> void Tree <T>::Insertchild(T value) {
    TreeNode<T>*newnode = new TreeNode<T>(value);
    if(current->firstchild == NULL) 
        current->firstchild = newnode;
    else {
        TreeNode<T>*p = current->firstchild;
        while ( p->nextsibling!=NULL)
            p = p->nextsibling;
        p->nextsibling = newnode;
    }
} 

2.8 森林

森林就是一坨树。

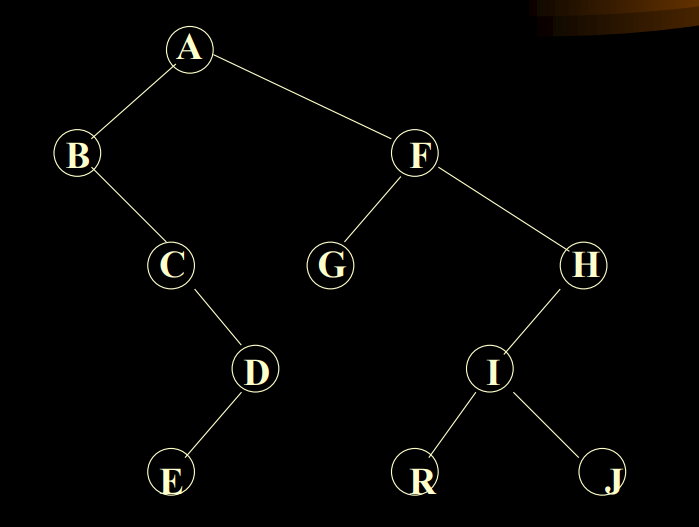
2.8.1 将森林转换成二叉树

每棵树转为二叉树
把每棵二叉树根用右链相连
2.8.2 森林的遍历
先根次序遍历（对应二叉树的先序）
- 访问F的第一棵树的根
- 按先根遍历第一棵树的子树森林
- 按先根遍历其它树组成的森林
中根次序遍历（对应二叉树的中序）
- 按中根遍历第一棵树的子树森林
- 访问F的第一棵树的根
- 按中根遍历其它树组成的森林
后根次序遍历（对应二叉树的后序）
- 按后根遍历第一棵树的子树森林
- 按后根遍历其它树组成的森林
- 访问F的第一棵树的根

2.9 Thread Tree 线索树

2.9.1 定义

目的:让二叉树遍历的速度更快
特点:在树的节点中加入一个指针(比如指向上一个节点)
n个结点的二叉树有2n个链域（指针存储的空间），其中真正有用的是n–1个，其它n+1个都是空域(null)。为了充分利用结点中的空域，使得对某些运算更快。
线索树根据添加的指针指向的结点不同，也会分为先序、中序、后序

（图例为中序线索树）

2.9.2 实现

2.9.3 按中序遍历中序线索树

按中序遍历，并且还是中序线索树，所以就很简单了。

遍历算法：

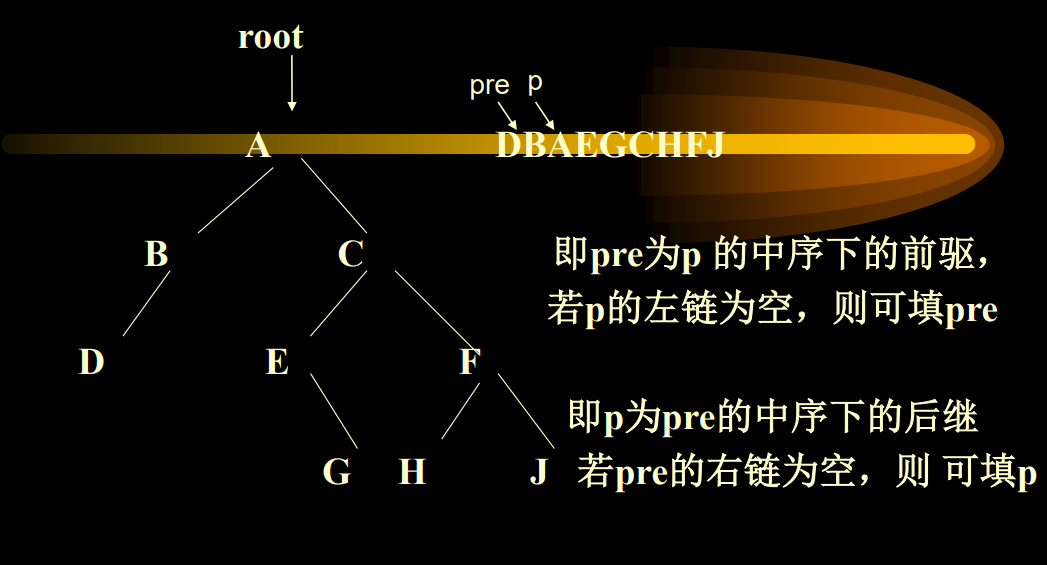
找到中序下的第一个结点（first）（注意笨笨们，这个不是根结点哦）
不断找后继（Next）
- 如果p结点没有右子树(p->rightthread == 1)则 p=p->rightchild(右链就是后继)
- p有右子树(p->rightThread==0) 则
  1. p=p->rightchild
  2. while(p->leftThread==0) p=p->leftchild;

2.9.4 构造中序线索树

与中序遍历算法差不多，但是要填左空域，右空域的前驱、后继指针。

加一个pre指针，它总是指向遍历指针p的中序下的前驱结点。

  
Void Inthread(threadNode<T> * T) {
    stack <threadNode <T>*> s(10)
    ThreadNode <T> *p = T ;
    ThreadNode <T> *pre = NULL;
    for (;;) {
        //查找到最左下部分的
        while (p!=NULL) {
            s.push(p);
            p = p ->leftchild;
        }
        //开始弹出栈
        if (!s.IsEmpty()){
            p = s.pop;
            if (pre != NULL) {
                //添加的代码，在这时候处理pre
                if (pre ->rightchild == NULL){
                    pre ->rightchild = p;  
                    pre ->rightthread = 1;
                }
                //处理p
                if( p -> leftchild == NULL) {
                    p -> leftchild = pre;
                    p ->leftthread = 1;
                }//添加的代码
            }
            pre = p ;
            p = p -> rightchild ;
        }
        else return;
    }//for 
}//建议把pre和p存储成全局变量

2.10 Huffman Tree 霍夫曼树

2.10.1 概念

增长树：
对原二叉树中度为1的结点，增加一个空树叶
对原二叉树中的树叶，增加两个空树叶
外通路长度(外路径)E：
根到每个外结点(增长树的叶子)的路径长度的总和（边数）
E=3+3+2+3+4+4+3+3=25
内通路长度（内路径）I：
根到每个内结点（非叶子）的路径长度的总和（边数）
结点的带权路径长度：一个结点的权值与根到该结点的路径长度的乘积。
- 每个结点的权重占有一定的值
带权的外路径长度：各叶结点的带权路径长度之和。
带权的内路径长度：各非叶结点的带权路径长度之和。

霍夫曼树：

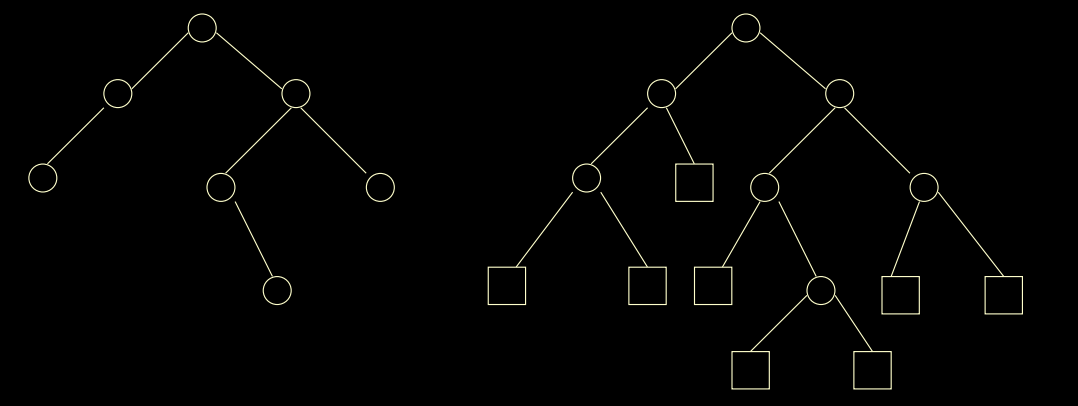
从形状上来讲，二叉树有以下三种大致形状。

第一幅图：11 * 1 + 2 * 4 + 3 * 2 + 3 * 3 = 34

2.10.2 Huffman 算法

如何构造霍夫曼树？

思想：权大的外结点靠近根，权小的远离根。

从m个权值中找出两个最小值W1，W2构成
把计算结果放进去和其他节点一起选出两个，进行迭代
内节点不会只有一个叶节点。

e.g：

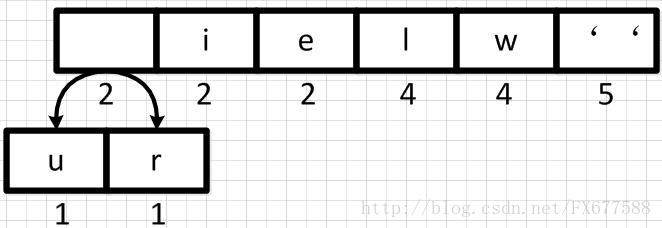
比方讲有这些结点，这些结点的权值从小到大排列

第一步取前两个先进行合并，两个元素相加作为新空元素，并且两者权重相加作为新元素的权重。

同理，新元素可以和字符i再合并

图新元素权重相加后结果是变大了，需要对权重进行重新排序。

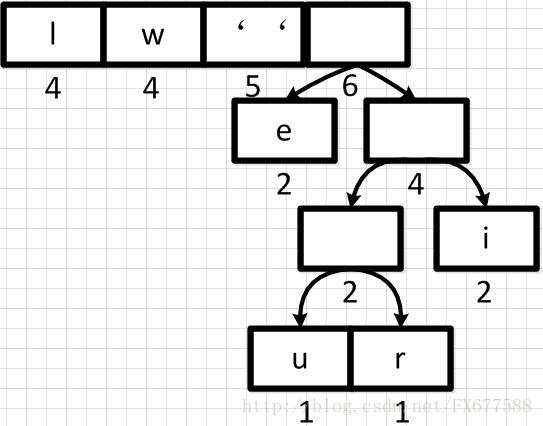
然后再依次从左到右合并，每合并一次则进行一次队列重新排序调整。

经过多步操作之后，得到以下的哈夫曼二叉树结构，也就是一个带有权重的二叉树：

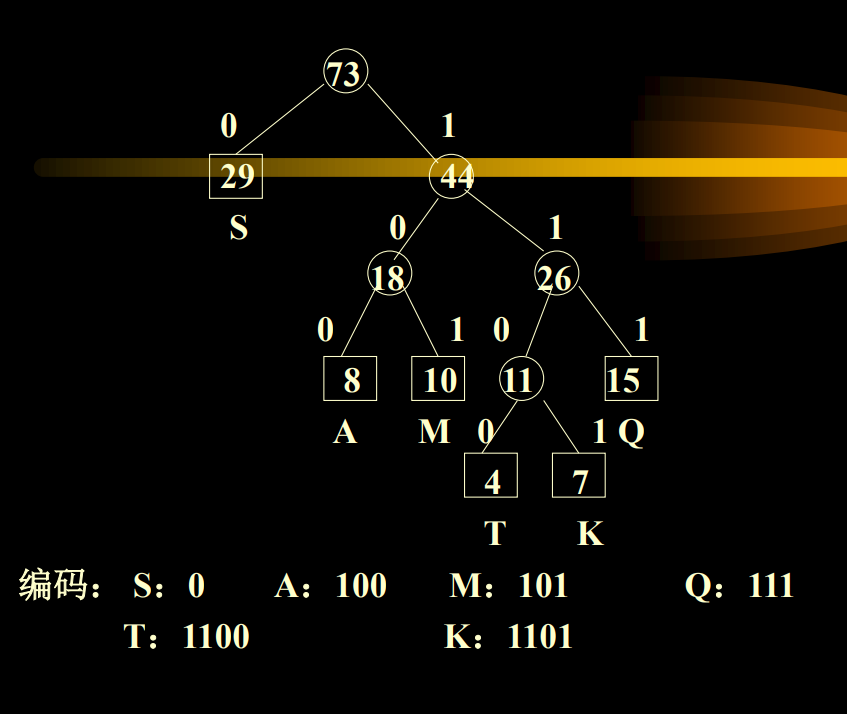
2.10.3 Huffman编码

是霍夫曼树在数据编码中一种应用。具体的讲用于通信的二进制编码中。设一电文出现的字符为D={M，S，T，A，Q， K}，每个字符出现的频率为W={10，29，4，8，15，7}，如何对上面的诸字符进行二进制编码，使得

该电文的总长度最短。
为了译码，任一字符的编码不应是另一字符的编码的前缀

利用Huffman算法，把{10，29，4，8，15，7}作为外部结点的权，构造具有最小带权外路径长度的扩充二叉树.

把每个结点的左子女的边标上0，右子女标上1。这样从根到每个叶子的路径上的号码连接起来，就是外结点的字符编码。

3. 考研例题

3.1 2019年

答案：D

答案：C

解析：第6层有8个叶结点，还可以有24个根结点呀。所以第7层有2 * 24 = 48个叶结点。前6层结点总和：2^6^-1。所以一共是48 + 2^6^-1 = 111

答案：B

解析：

1：A和C

2：B和D

3：记住：左子女右兄弟，不可能发生3的情况

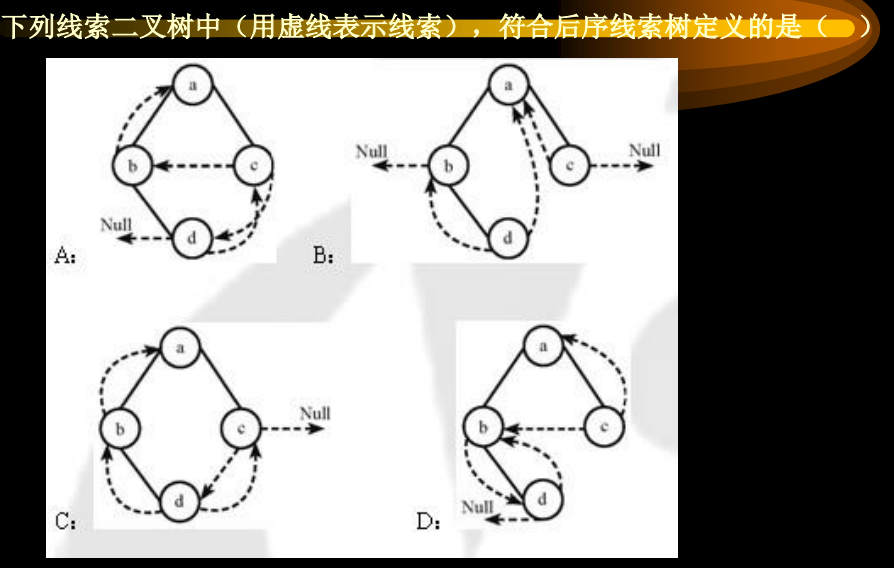
3.2 2020年